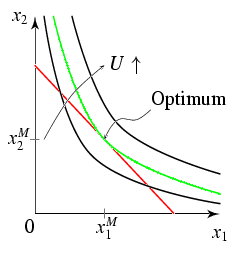
Der optimale Verbrauchsplan: Analytische Bestimmung
Nutzenmaximierung
ökonomisches Prinzip
Restriktion als Ungleichung
Problem der Maximierung einer
Nutzenfunktion $u(x_1, x_2)$
unter der Nebenbedingung eines gegebenen Einkommens $y$, wobei die
Nebenbedingung als Gleichung vorliegt.
\begin{eqnarray*}
&&u(x_1, x_2) \to \text{Max.}\\
\text{u.d.NB.}\quad &&p_1x_1 + p_2x_2 = y\\
&& x_1, x_2\geq 0
\end{eqnarray*}
Grafische Darstellung der Lösung:
Lagrange-Ansatz:
\[
\cL(x_1, x_2, \lambda) = u(x_1, x_2) + \lambda (y - p_1x_1 - p_2x_2)
\]
Unbekannte: $x_1$, $x_2$, $\lambda=$ Lagrange-Multiplikator
Parameter: $p_1$, $p_2$, $y$ sind zunächst als Konstante zu behandeln.
Entscheidend: $\cL$ nimmt in Bezug auf $x_1$, $x_2$ das Maximum dort an, wo
auch die Zielfunktion $u$ maximal ist (und umgekehrt).
- Bedingungen 1. Ordnung oder Lagrange-Bedingungen: partielle Ableitungen
gleich Null setzen.
Damit erhält man ein Gleichungssystem aus 3 Gleichungen mit 3 Variablen
$x_1$, $x_2$ und $\lambda$.
- Bedingungen 2. Ordnung (Min. oder Max.): hier nicht berücksichtigt!
Notwendige Bedingungen 1. Ordnung (3 Gleichungen, 3 Variablen)
\begin{eqnarray*}
\abl{\cL}{x_1} &=& \abl{u(x_1^*, x_2^*)}{x_1} - \lambda^* p_1 = 0\\
\abl{\cL}{x_2} &=& \abl{u(x_1^*, x_2^*)}{x_2} - \lambda^* p_2 = 0\\
\abl{\cL}{\lambda} &=& y - p_1x_1^* - p_2x_2^* = 0
\quad\text{Nebenbedingung des Problems}
\end{eqnarray*}
Aus den beiden ersten Gleichungen lässt sich $\lambda^*$ eliminieren
\[
\frac{{\partial}u/{\partial}x_1}{{\partial}u/{\partial}x_2} = \frac{p_1}{p_2}
\quad\text{oder}\quad
\frac{{\partial}u/{\partial}x_1}{p_1} = \frac{{\partial}u/{\partial}x_2}{p_2}
= \lambda^*
\]
Die linke Gleichung zur Grenzrate der Substitution
(GRS)
besagt, dass sich die Grenznutzen wie die Güterpreise
verhalten. Die rechte Aussage entspricht der modernen Fassung des
2. Gossenschen Gesetzes; Gesetz vom Ausgleich der
Grenznutzen des Geldes.
Also liegen 2 Gleichungen mit 2 Variablen (nämlich $x_1^*$, $x_2^*$) vor:
\begin{eqnarray*}
\text{Tangentialpunkt}
&& GRS
= \frac{{\partial}u/{\partial}x_1}{{\partial}u/{\partial}x_2}
= -\frac{\d x_2}{\d x_1} = \frac{p_1}{p_2}.\\
\text{auf der Budgetgleichung}
&&y = p_1x_1^*+p_2x_2^*
\end{eqnarray*}
Aufgrund der Eigenschaften der Nutzenfunktion und der Bilanzgleichung
(konstante Preise) liefert das
Gleichungssystem
Setzt man die Marshallschen Nachfragefunktionen in die Zielfunktion ein, dann
ergibt sich die
indirekte Nutzenfunktion
als Lösung des Problems.
Man beachte, dass die Lösung von den Parametern $p_1$, $p_2$ und $y$ des
Problems abhängt. Wird einer der Güterpreise variiert, dann ändert sich auch
die Lösung. Dieser Tatbestand wird durch die
Preis-Konsum-Kurve erfasst. Der analoge Effekt einer
Änderung des Einkommens wird mit Hilfe der
Einkommen-Konsum-Kurve bzw. den
Engel-Kurven
beschrieben.
intertemporale Nutzenmaximierung
Arbeitsangebot