$\def\cL{\mathcal{L}}$ $\def\abl#1#2{\frac{\partial #1}{\partial #2}}\def\d{\textrm{d}}$

Der optimale Verbrauchsplan: Analytische Bestimmung

Intertemporale Nutzenmaximierung

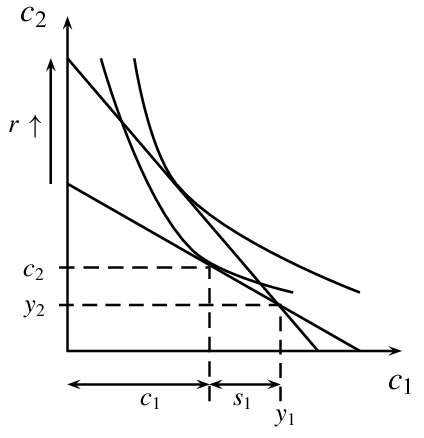
Problem der Maximierung einer Nutzenfunktion $u(e_t,e_{t+1})$ unter der Nebenbedingung gegebener Einkommen $y_t$ und $y_{t+1}$. Die beiden Nebenbedingungen liegen als Gleichungen vor und lauten \begin{eqnarray*} \text{Periode} t &\quad&y_t = e_t+s_t\\ \text{Periode} t+1&\quad&y_{t+1}+(1+r) s_t = e_{t+1} \end{eqnarray*} Wenn in der ersten Periode $t$ weniger ausgibt wird als das Einkommen es erlaubt, $e_t < y_t$, dann spart der Haushalt, $s_t>0$. Diese Ersparnis steht in der nächsten Periode einschließlich der Verzinsung (Zinssatz $r$) zur Verfügung. Der heutige Konsum (oder die heutigen Ausgaben) wird damit in die Zukunft verlagert. Dieser Vorgang ist prinzipiell auch umgekehrt möglich. Wenn man auf das zukünftige (sicher gegebene) Einkommen $y_{t+1}$ einen Kredit aufnimmt, dann gilt $s_t<0$ bzw. $e_t>y_t$. In beiden Fällen wird derselbe Zinssatz $r$ unterstellt.
Um eine Variable (und eine Gleichung) weniger handhaben zu müssen, wird zunächst die Ersparnis $s_t$ aus den beiden Nebenbedingungen eliminiert. \[ y_{t+1} + (1+r) (y_t-e_t) = e_{t+1} \] Damit lautet das Problem der intertemporalen Nutzenmaximierung \begin{eqnarray*} &&U = u(e_t,e_{t+1}) \to \text{Max.}\\ \text{u.d.NB.}\quad &&(1+r)e_t+e_{t+1} = (1+r)y_t+y_{t+1}\\ &&e_t, e_{t+1}\geq 0 \end{eqnarray*} Lagrange-Ansatz \[ \cL(e_t,e_{t+1},\lambda) = u(e_t,e_{t+1}) + \lambda ( (1+r)y_t+y_{t+1}-(1+r)e_t-e_{t+1} ) \] Unbekannte: $e_t$, $e_{t+1}$, $\lambda=$ Lagrange-Multiplikator
Parameter: $y_t$, $y_{t+1}$, $r$ sind zunächst als Konstante zu behandeln.
Entscheidend: $\cL$ nimmt in Bezug auf $e_t$, $e_{t+1}$ das Maximum dort an, wo auch die Zielfunktion $u$ maximal ist (und umgekehrt).
  1. Bedingungen 1. Ordnung oder Lagrange-Bedingungen: partielle Ableitungen gleich Null setzen.
    Damit erhält man ein Gleichungssystem aus 3 Gleichungen mit 3 Variablen $e_t$, $e_{t+1}$ und $\lambda$.
  2. Bedingungen 2. Ordnung (Min. oder Max.): hier nicht berücksichtigt!
Notwendige Bedingungen 1. Ordnung (3 Gleichungen, 3 Variablen) \begin{eqnarray*} \abl{\cL}{e_t} &\ =\ & \abl{u(e_t^*,e_{t+1}^*)}{e_t} - \lambda^* (1+r) = 0\\ \abl{\cL}{e_{t+1}} &\ =\ & \abl{u(e_t^*,e_{t+1}^*)}{e_{t+1}} - \lambda^* = 0\\ \abl{\cL}{\lambda} &\ =\ & (1+r)y_t+y_{t+1}-(1+r)e_t-e_{t+1} = 0 \quad\text{Budgetrestriktion} \end{eqnarray*} Aus den beiden ersten Gleichungen lässt sich $\lambda^*$ eliminieren \[ \frac{{\partial}u/{\partial}e_t}{{\partial}u/{\partial}e_{t+1}}\ = 1+r \quad\text{oder}\quad \frac{{\partial}u/{\partial}e_t}{1+r}\ = \ {\partial}u/{\partial}e_{t+1}\ = \lambda^* \] Die Grenznutzen verhalten sich wie der Zinsfaktor ($1+r$). Oder äquivalent, Gleichheit der mit dem Zinsfaktor gewichteten Grenznutzen des Konsums $= \lambda^*$ (intertemporale Version des 2. Gossenschen Gesetzes).
Also liegen 2 Gleichungen mit 2 Variablen (nämlich $e_t^*$ ,$e_{t+1}^*$) vor: \begin{eqnarray*} \text{Tangentialpunkt}\quad &&\text{GRiS}\ =\ \frac{{\partial}u/{\partial}e_t}{{\partial}u/{\partial}e_{t+1}} \ = -\ \frac{\d e_{t+1}}{\d e_t} = 1+r\\ \text{auf der Budgetgeraden}\quad &&(1+r)y_t + y_{t+1} = (1+r)e_t + e_{t+1} \end{eqnarray*} Aufgrund der Eigenschaften der Nutzenfunktion (abnehmende GRiS) und der Bilanzgleichung (gegebene Einkommen) liefert das Gleichungssystem
Abb. Grenzrate der intertemporalen Substitution
Nutzenmaximierung
Arbeitsangebot