Privatdozent Dr. Hagen Bobzin

Startseite Volkswirtschaftslehre Lebenslauf Veröffentlichungen Mikroökonomik Makroökonomik Mathematik für Ökonomen Netzwerkökonomik Vorlesungen Impressum Mikroökonomik Index Symbole Übersicht Theorie des Haushalts Theorie der Unternehmung

Nutzenmaximales Arbeitsangebots

Problem der Maximierung einer Nutzenfunktion $u(x,F)$ unter der Nebenbedingung einer gegebenen Zeit pro Periode, wobei die Nebenbedingung als Gleichung vorliegt. Die Nutzenfunktion hängt vom Konsum $x$ (Konsumausgaben $e=px$) und der Freizeit $F$ ab. Pro Tag sind 16 Stunden zu disponieren (bei 8 Stunden Schlaf). Jede Stunde Freizeit kostet eine Stunde Arbeitszeit $L$ (Opportunitätskosten). Bei dem Lohnsatz $w$ (Euro/Stunde) ergibt sich das Einkommen $y$, das mit den Ausgaben $e$ übereinstimmt. \begin{eqnarray*} &&U = u(x,F) \to \text{Max.}\\ \text{u.d.NB.}\quad &&A + F = 16\\ &&y = wA\\ &&y = px\\ &&A,F,x\geq 0 \end{eqnarray*} Eliminiert man die Variablen $y$ und $A$, dann stellt sich eine einzige Nebenbedingung ein: \[ \frac{px}{w} + F = 16\quad\text{oder}\quad px + wF = w16 \] Lagrange-Ansatz \[ \cL(x,F,\lambda) = u(x,F) + \lambda (w16-px-wF) \] Unbekannte: $x$, $F$, $\lambda=$ Lagrange-Multiplikator
Parameter: $p$, $w$ sind zunächst als Konstanten zu behandeln. Entscheidend: $\cL$ nimmt in Bezug auf $x$, $F$ das Maximum dort an, wo auch die Zielfunktion $u$ maximal ist (und umgekehrt).

1. Bedingungen 1. Ordnung oder Lagrange-Bedingungen: partielle Ableitungen gleich Null setzen.
   Damit erhält man ein Gleichungssystem aus 3 Gleichungen mit 3 Variablen $x$, $F$ und $\lambda$.
2. Bedingungen 2. Ordnung (Min. oder Max.): hier nicht berücksichtigt!

Notwendige Bedingungen 1. Ordnung (3 Gleichungen, 3 Variablen) \begin{eqnarray*} \abl{\cL}{x} &=& \abl{u(x^*,F^*)}{x} - \lambda^* p = 0\\ \abl{\cL}{F} &=& \abl{u(x^*,F^*)}{F} - \lambda^* w = 0\\ \abl{\cL}{\lambda} &=&w16-px^*-wF^* = 0 \quad\text{Nebenbedingung des Problems} \end{eqnarray*} Aus den beiden ersten Gleichungen lässt sich $\lambda^*$ eliminieren \[ \frac{{\partial}u/{\partial}F}{{\partial}u/{\partial}x} = \frac{w}{p} \quad\text{oder}\quad \frac{{\partial}u/{\partial}x}{p}= \frac{{\partial}u/{\partial}F}{w}=\lambda^* \] Die Grenznutzen verhalten sich wie der (Real-)Lohnsatz. Oder äquivalent, Gleichheit der Grenznutzen des Geldes $= \lambda^*$ (2. Gossensche Gesetz). Also liegen 2 Gleichungen mit 2 Variablen (nämlich $x^*$ ,$F^*$) vor: \begin{eqnarray*} \text{Tangentialpunkt}\quad &\text{GRS}=\frac{{\partial}u/{\partial}F}{{\partial}u/{\partial}x}=-\frac{\d x}{\d F}=\frac{w}{p}.\\ \text{auf der Budgetgleichung} \quad &w16=px^*+w^*F \end{eqnarray*} Aufgrund der Eigenschaften der Nutzenfunktion (abnehmende GRS) und der Restiktion (konstanter Lohnsatz) liefert das Gleichungssystem

• die optimale Konsumsumme und die Nachfrage nach Freizeit \[ x^*=x(p,w) \quad\text{und}\quad F^*=F(p,w) \]
• das Arbeitsangebot: \[ A^*(p,w) = 16 - F^*(p,w) \]
• den optimalen Wert des Lagrange-Multiplikators $\lambda^*=\lambda(p,w)$. (ökonomische Interpretation)

Beispiel für eine resultierende Lohn-Freizeit-Kurve Setzt man die Nachfragefunktionen in die Zielfunktion ein, dann ergibt sich die indirekte Nutzenfunktion als Lösung des Problems. Nutzenmaximierung
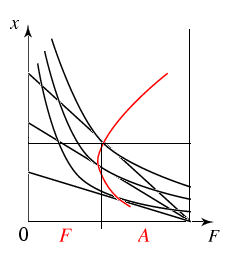
intertemporale Nutzenmaximierung