Nutzenfunktion
Zu den Voraussetzungen für die Existenz einer stetigen Nutzenfunktion
\[
U = u(x_1,x_2)
\]
siehe unter
Präferenzen.
Kardinaler Nutzen
Jedes Güterbündel ist mit einem bestimmten Grad der
Bedürfnisbefriedigung also einem Nutzenniveau verbunden. Werden die
Präferenzen durch eine Nutzenfunktion repräsentiert, die das Nutzenniveau in
Nutzeneinheiten angibt, so spricht man von einer kardinalen Nutzenfunktion.
In diesem Fall lassen sich inbesondere Nutzendifferenzen messen, so wie es
die Berechnung des Grenznutzens vermuten lässt.
1. Gossensches Gesetz
Ordinaler Nutzen
Mit der axiomatischen Beschreibung von Präferenzen wird der Grundstein für
die ordinale Nutzenmessung gelegt. Von der Nutzenfunktion $u$ wird lediglich
verlangt, dass sie indexerhaltend ist,
\[
\vx' \geq_P \vx'' \iff u(\vx') \geq u(\vx')
\]
Da Nutzendifferenzen nun keine Rolle mehr spielen, beschreibt auch jede
monotone Transformation der
Nutzenfunktion $u$ dieselben Präferenzen.
Anmerkungen
Der Grenznutzen selber spielt in der modernen mikroökonomischen Theorie eine
untergeordnete Rolle, sofern man sich auf die Änderung des
Nutzenniveaus konzentriert.
Dagegen ist das Verhältnis der Grenznutzen von entscheidender Bedeutung,
denn es gibt Auskunft über den Verlauf einer Indifferenzkurve, auf der das
Nutzenniveau konstant ist.
Zur approximativen Messung von Nutzendifferenzen in Geldeinheiten siehe
money metric utility function
Geschichte der Nutzentheorie (englisch)
Zur Vereinfachung der Analyse wird unterstellt, dass die stetige
Nutzenfunktion außerdem
differenzierbar ist.
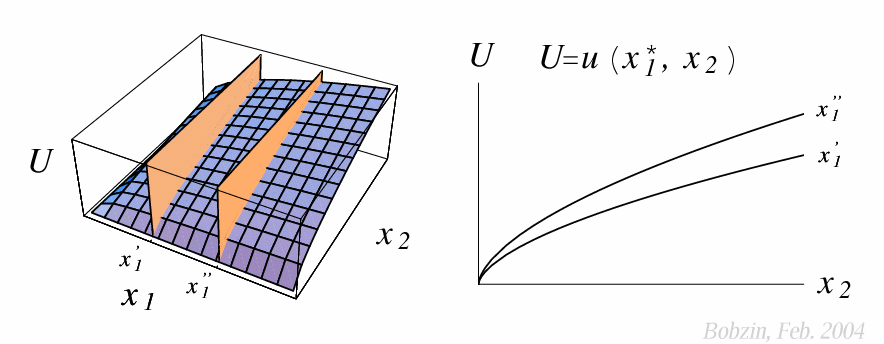
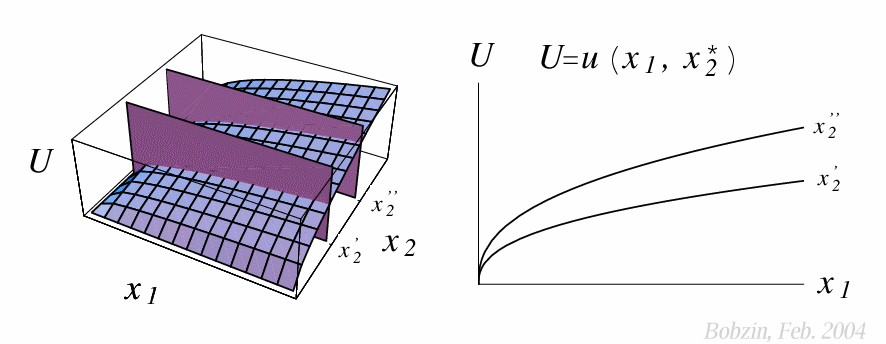
Schnitte durch das Nutzengebirge:
- $U = u(x_1', x_2)$ und $U = u(x_1'', x_2)$ mit $x_1''>x_1'$
- $U = u(x_1, x_2')$ und $U = u(x_1, x_2'')$ mit $x_2''>x_2'$
- Die implizite Indifferenzkurve
$U^K = u(x_1, x_2)$ für das konstante Nutzenniveau $U^K$ lautet in expliziter Form:
\[
x_2 = u^{-1}(x_1, U^K) \implies x_2 = g(x_1)
\]
Eine grafische Darstellung der entsprechenden Schnittfläche findet man bei
der Behandlung der Indifferenzkurven.
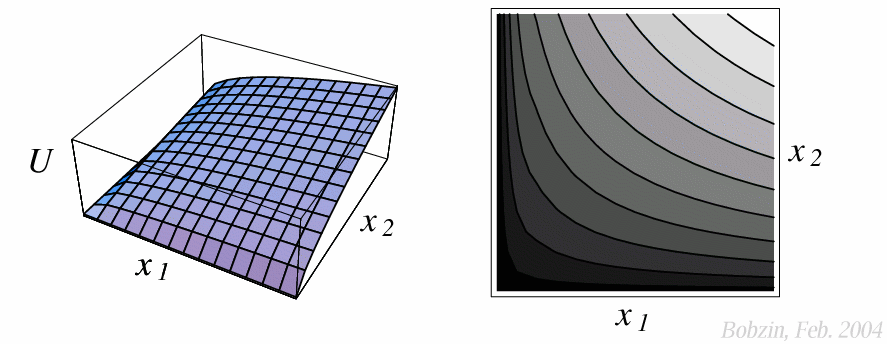
Ähnlich den Höhenlinien einer Landschaft ergibt sich ein System von
Indifferenzkurven.
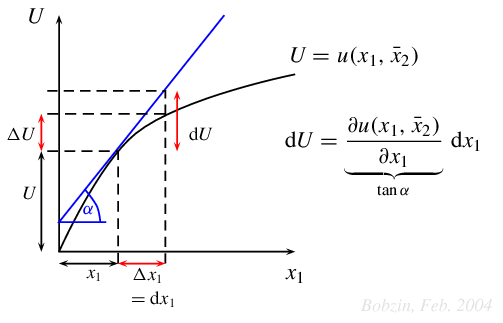
Der
Grenznutzen des Gutes $j$
\[
\abl{u(x_1^*,x_2^*)}{x_j}>0 \quad\text{mit}\quad j=1,2
\]
gibt an, wie das Nutzenniveau $U = u(x_1^*,x_2^*)$ reagiert, wenn die
Menge des Gutes $j$, also $x_j^*$, marginal verändert wird. In der
Regel wird von Nichtsättigung ausgegangen, so dass die Grenznutzen
positiv sind, d.h., zusätzliche Gütermengen verbessern das
Wohlbefinden.
Entsprechend dem
1. Gossensches Gesetz wird
unterstellt, dass die zweite Ableitung negativ ist
\[
\abl{^2 u(x_1^*,x_2^*)}{x_j^2}>0 \quad\text{mit}\quad j=1,2.
\]
Damit nimmt der Grenznutzen des Gutes $j$ mit wachsendem Verbrauch ab.
Die
Steigung $g'(x_1)$ einer Indifferenzkurve
(
GRS) lässt sich über den
Satz der impliziten Differentiation
bestimmen.