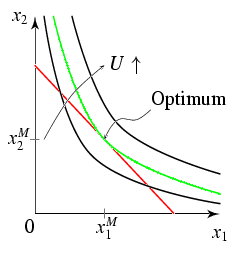
Marshallsche Funktionen der Güternachfrage
Die
Nutzenmaximierung generiert die Marshallschen
oder gewöhnlichen Nachfragefunktionen
\[
x_1^* = x_1^M(p_1, p_2, y) \UND x_2^* = x_2^M(p_1, p_2, y);
\]
Diese Funktionen sind
homogen vom Grade null in p1, p2
und y, denn eine Vervielfachung des Einkommens und der Preise um einen
Faktor
k > 0, lässt nicht nur die Zielfunktion $u(x_1, x_2)$, sondern auch die
Budgetrestriktion
\[
(k y) = (k p_1)x_1 + (k p_2)x_2 \implies y = p_1x_1 + p_2x_2
\]
unverändert. Da der Haushalt merkt, dass der Faktor
k seine
Entscheidungssituation nicht beeinflusst (das Einkommen wächst im selben
Ausmaß wie die Ausgaben), behält er den ursprünglichen Konsumplan bei: Er
handelt
frei von Geldillusion.
Setzt man die Marshallschen Funktionen in die Nutzenfunktion ein, so
resultiert die
indirekte Nutzenfunktion.
Ist lediglich die indirekte Nutzenfunktion bekannt, dann können die
Marshallschen Funktionen über
Roys Identität berechnet
werden.
Hickssche Güternachfrage