Computergestützte Lehre der Makroökonomik
 Artikel als PDF
Artikel als PDF
 Gliederung der Vorlesung Makroökonomik I
Gliederung der Vorlesung Makroökonomik I
 Das Software-Paket
Das Software-Paket
 Copyright (GNU General Public License)
Copyright (GNU General Public License)
PD Dr. Hagen Bobzin
Fachbereich 5, Wirtschaftswissenschaften
Universität Siegen
57068 Siegen
Schlüsselbegriffe: Makroökonomik, computergestützte Lehre
JEL classification: A20, E12, F40, O40
e-mail:
Bobzin@vwl.wiwi.uni-siegen.de
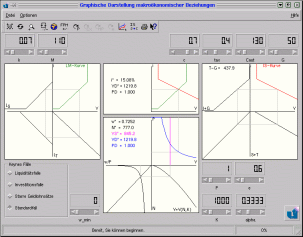 Gesamtübersicht. Gesamtübersicht. |
 Detailansicht |
Inhaltsvereichnis
1 Computergestützte Lehre der makroökonomischen Theorie
2 Das Gleichgewicht auf dem Gütermarkt
2.1 Grundlegende Definitionen der volkswirtschaftlichen Gesamtrechnung
2.2 Die Nachfrage auf dem Gütermarkt
2.2.1 Der Konsum
2.2.2 Die Investition
2.2.3 Die Staatsausgaben
2.3 Die Bestimmung des Gleichgewichts
2.3.1 Sparsicht
2.3.2 Konsumsicht
2.3.3 Eigenschaften der IS-Kurve
3 Das Gleichgewicht auf dem Geldmarkt
3.1 Die Geldnachfrage
3.2 Das Geldangebot
3.3 Die Bestimmung des Gleichgewichts
3.3.1 Die Ableitung der LM-Kurve
3.3.2 Eigenschaften der LM-Kurve
3.3.3 Der klassische Bereich der LM-Kurve
4 Die gesamtwirtschaftliche Endnachfrage
4.1 Das simultane Gleichgewicht auf dem Güter- und Geldmarkt
4.2 Ableitung der gesamtwirtschaftlichen Endnachfrage
5 Das gesamtwirtschaftliche Angebot
5.1 Der Produktionssektor
5.2 Der Arbeitsmarkt
6 Das gesamtwirtschaftliche Gleichgewicht
6.1 Die Lösung des Modells
6.1.1 Formale Aspekte des interdependenten Gleichungssystems
6.1.2 Der Preismechanismus
6.2 Das Walras-Gesetz
6.3 Die Keynes-Fälle
6.3.1 Die Liquiditätsfalle
6.3.2 Die Investitionsfalle
6.3.3 Nach unten starre Geldlohnsätze
7 Erweiterungen
7.1 Die offene Volkswirtschaft
7.1.1 Das modifizierte Kontensystem
7.1.2 Der modifizierte Gütermarkt
7.1.3 Die Weltmärkte
7.1.4 Mechanismen zum Ausgleich der Zahlungsbilanz
7.2 Wirtschaftswachstum
1 Computergestützte Lehre der makroökonomischen Theorie
Bis zum heutigen Tag begnügen sich die meisten Lehrbücher der makroökonomischen Theorie damit, den Studierenden die mathematischen Grundlagen und ihre Implikationen anhand von Schaubildern zu erklären. Dabei wird auf virtuose Weise beschrieben, wie sich Verschiebungen und Drehungen von Kurven ökonomisch auswirken. Häufig findet man sogar ganze Systeme von Quadranten, deren Interdependenzen kaum noch zu überschauen sind (Dernburg, McDougall (1981,S. 135]). Der vorliegende Beitrag hat das Ziel, dem Studierenden mit Hilfe des Computers zu zeigen, wie sich das Gleichungssystem eines keynesianischen Makromodells visuell veranschaulichen lässt. Damit unterscheidet sich der Ansatz von Anderson (1993) , wo die Betonung auf der symbolischen Berechnung liegt. Andere Arbeiten wie Mercado, Kendrick, Amman (1998) beklagen, dass die Programmierung für den Studierenden vollkommen undurchsichtig bleibt. Sie stellen daher ein Programm vor, bei dem der Studierende selbst, das entsprechende Gleichungssystem eingibt, wobei im Wesentlichen numerischer Output erzeugt wird. Obwohl der Sourcecode des hier vorgestellten Programms frei verfügbar ist, wird die eigentliche Programmierung nur eine untergeordnete Rolle spielen.
Als Beispiel ist ein einfaches makroökonomisches Modell keynesianischer Prägung gewählt worden, wie es bereits in den ersten Semestern eingeführt wird. Dabei konzentriert sich das Programm auf solche Effekte, die sich auf Grund von Änderungen der Parameter oder der Instrumentvariablen einstellen. Das Preisniveau als endogene Variable spielt eine gesonderte Rolle, um inflatorische Vorgänge auf dem Weg hin zu einem simultanen gesamtwirtschaftlichen Gleichgewicht besser darstellen zu können. Exemplarisch wird das Modell einer geschlossenen Volkswirtschaft mit staatlicher Aktivität um einzelne Aspekte ergänzt. Zum einen lässt sich eine offene Volkswirtschaft berücksichtigen, so dass Handelsbeziehungen abgebildet werden können. Hier werden die Ausgleichsmechanismen der Zahlungsbilanz eine besondere Rolle spielen. Zum anderen ist es möglich, Vorgänge des ökonomischen Wachstums darzustellen.
Man beachte, dass das Programm zu didaktischen Zwecken auf sehr einfachen Annahmen beruht, wobei viele Grundlagen in Otruba, Munduch, Stiassny (1996) wiederzufinden sind. Ergänzende Inhalte lassen sich den Lehrbüchern von Sachs, Larrain (1993) oder auch Mankiw (1998) entnehmen. Insbesondere die Ableitung des Weltimportmarktes und des Weltexportmarktes kann in Siebert (1994) nachgelesen werden. Die Wachstumsvorgänge lehnen sich an das neoklassische Modell von Solow und Swan an, wie es in Barro, Sala-i-Martin (1998) geschildert wird.
Für Hinweise und Anregungen steht der Autor jederzeit zur Verfügung (e-mail: Bobzin). Allerdings sollte bedacht werden, dass sich der Beitrag in erster Linie an Studierende richtet, um ihnen das Zusammenwirken der verschiedenen aggregierten Märkte zu verdeutlichen. In der vorliegenden Fassung kann das Programm nur andeuten, wie sich weiterführende Theorien der Makroökonomik integrieren lassen.
Zum eigentlichen Computerprogramm ist anzumerken, dass es in C++ geschrieben worden ist und auf den Bibliotheken von Qt 5.7 basiert. Diese Software ist frei verfügbar und wird häufig als GUI-Entwicklungsumgebung für Linux eingesetzt. Neben dem online manual hat Lehnert (1999) ein gut strukturiertes Handbuch zur Verfügung gestellt. Geeignete Software vorausgesetzt ist es möglich, den Quellcode auch unter Windows zu kompilieren. Damit steht außer der Linux-Version auch eine lauffähige Version für Windows zur Verfügung. Sollte Interesse am eigentlichen Quellcode bestehen, um eigene Ideen zu verwirklichen, kann man die jeweils aktuelle und dokumentierte Software hier herunterladen.
2 Das Gleichgewicht auf dem Gütermarkt
2.1 Grundlegende Definitionen der volkswirtschaftlichen Gesamtrechnung
Für die volkswirtschaftliche Kreislaufanalyse einer geschlossenen
Volkswirtschaft mit staatlicher Aktivität sind zunächst drei
gesamtwirtschaftliche Konten von zentraler Bedeutung, nämlich das
Produktionskonto (1), das Einkommenskonto (2) sowie
das Finanzierungskonto1
(3).
| ||||||||||||
Da Abschreibungen unberücksichtigt bleiben, bezeichnet I die
Nettoinvestition. Solange der Staat keine indirekten Steuern erhebt, stimmen
die Verkaufserlöse, also der private Konsum C, die private Investition I
und die Ausgaben des Staates
|
mit dem Faktoreinkommen bzw. dem Nettoinlandsprodukt Y überein. Ohne
außenwirtschaftliche Beziehungen unterscheidet sich Y nicht vom
Nettonationaleinkommen. Dieses sogenannte Volkseinkommen spiegelt die
Faktoreinkommen wider, auf die direkte Steuern T zu zahlen sind. Die
Steuereinnahmen werden zur Deckung der Staatausgaben G benötigt, wobei der
Staat den Teil CSt konsumiert und den Rest SSt = T−CSt für
öffentliche Investitionen ISt ausgibt. Das resultierende verfügbare
Einkommen des privaten Sektors Yv = Y−T wird ebenfalls zu Konsumzwecken C
verwendet, wobei das Residuum die Ersparnis S bezeichnet. Die Gleichung
(3) stellt die einkommenschaffenden Tatbestände I+ISt den
einkommenvernichtenden Tatbeständen S+SSt gegenüber. Die vertrautere Form
| (4) |
ergibt sich, indem man CSt auf beiden Seiten der Gleichung (3)
addiert. In Bezug auf das buchungstechnische Resultat (4) mag
es hilfreich sein, den staatlichen Konsum ganz zu vernachlässigen,
CSt = 0. Hält sich der Staat an seine Budgetgleichung, dann gilt
ISt = G = T = SSt. Ohne diese Annahme gehen in (4) sämtliche
Informationen über die Kreditverflechtung zwischen dem privaten Sektor und dem
Staat verloren. Alternativ stellt sich das Ergebnis (4)
auch dann ein, wenn man das Produktionskonto Y = C+I+G und das Einkommenskonto
des privaten Sektors C+S = Y−T konsolidiert.
Ohne Staat erhält man die vertrautere ex-post Identität als
|
die sich auch dann ergibt, wenn der Staat weder investiert noch spart, ISt = SSt = 0.
2.2 Die Nachfrage auf dem Gütermarkt
2.2.1 Der Konsum
Entsprechend der von J. M. Keynes eingeführten
absoluten Einkommenshypothese wird unterstellt, dass die Konsumnachfrage der
Haushalte linear mit dem verfügbaren Einkommen Yv steigt,
C(Yv) = C0+cYv, wobei Yv = Y−T(Y). Darin bezeichnet C0 den autonomen
Konsum und dC/dYv = c die marginale Konsumquote. Außerdem erhebt der
Staat eine Einkommensteuer T(Y) = tY mit dem Steuersatz t, um Einnahmen zu
erzielen.
Die resultierende Konsumfunktion
| (5) |
enthält demnach die Parameter C0, c und t. In der Kopfzeile der
Abbildung 1 werden die zugehörigen numerischen Werte unter (1),
(2) und (3) angezeigt.2
Demnach gilt derzeit für die marginale Konsumquote c = 0,7, der Steuersatz
ist auf tax ≡ t = 0,4 gesetzt worden und der autonome Konsum
hat den Wert Caut = C0 = 130. Sämtliche Variablen können mit Hilfe
der Schieberegler
![]() modifiziert werden, die über den jeweiligen Variablen zu
sehen sind. Die entsprechenden Effekte werden unmittelbar grafisch
umgesetzt. Über das Icon
modifiziert werden, die über den jeweiligen Variablen zu
sehen sind. Die entsprechenden Effekte werden unmittelbar grafisch
umgesetzt. Über das Icon
![]() lassen sich die Ausgangswerte
jederzeit wieder herstellen.
lassen sich die Ausgangswerte
jederzeit wieder herstellen.
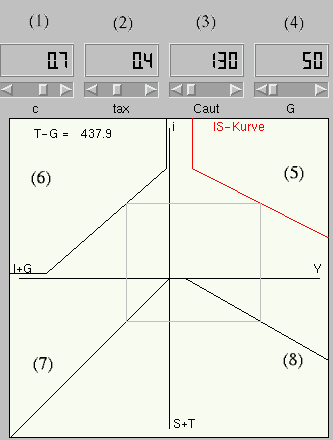 Abbildung 1: Das Gleichgewicht auf dem Gütermarkt
Abbildung 1: Das Gleichgewicht auf dem Gütermarkt
2.2.2 Die Investition
Im Quadranten (6) ist neben den
konstanten Staatsausgaben G eine zinsabhängige Investitionsfunktion
dargestellt, die der folgenden Vorschrift genügt:
| (6) |
Der positive Parameter ρ drückt aus, dass die Investition mit steigendem
Zinssatz im Bereich i1 ≤ i ≤ i2 abnimmt. Die Ableitung einer solchen
Keynesschen Investitionsfunktion aus statischer Sicht kann man in
Woll (2000,S. 359 ff.] nachlesen, wo die optimale Investition als
Differenz zwischen dem optimalen und dem aktuellen Kapitalstock K ermittelt wird.
Das entsprechende Problem der dynamischen Optimierung ist Sargent (1994, S. 131
ff.] zu entnehmen. In beiden Fällen verschwindet die Investition
vollständig, sobald der reale3
Zinssatz i die Grenzleistungsfähigkeit des Kapitals (P/PK) ∂Y/∂K bzw. i2 übersteigt.
![]() Die mit i1 und i2 bezeichneten Knickstellen können variiert werden, indem
der Benutzer seine Maus in den Quadranten (6) führt. Bei gedrückter
linker Maustaste lässt sich die untere linke Ecke horizontal bewegen. Analog
kann die obere Ecke vertikal verschoben werden, indem man die rechte Maustaste
gedrückt hält. Die implizite Änderung des Parameters ρ wird automatisch
in die entsprechenden grafischen Effekte umgesetzt.
Die mit i1 und i2 bezeichneten Knickstellen können variiert werden, indem
der Benutzer seine Maus in den Quadranten (6) führt. Bei gedrückter
linker Maustaste lässt sich die untere linke Ecke horizontal bewegen. Analog
kann die obere Ecke vertikal verschoben werden, indem man die rechte Maustaste
gedrückt hält. Die implizite Änderung des Parameters ρ wird automatisch
in die entsprechenden grafischen Effekte umgesetzt.
2.2.3 Die Staatsausgaben
Neben der Investition enthält der Quadrant (6) auch die Staatsausgaben G, die sich wie eine vollständige Verschiebung von I(i) auswirken. Unter (4) kann der derzeitige Wert für die Staatsausgaben G = 50 im Sinne der Fiskalpolitik abgeändert werden.
2.3 Die Bestimmung des Gleichgewichts
2.3.1 Sparsicht
Zunächst ist zu berücksichtigen, dass die ex post Identität (ohne staatliche Aktivität) I ≡ S jederzeit erfüllt ist. Dabei bezieht sich die Identität auf die realisierte Investition I, die die geplante und die ungeplante Investition enthält. Der Gütermarkt befindet sich jedoch nur dann in einem Gleichgewicht, wenn alle ungeplanten Tatbestände verschwinden (Mankiw (1998, S. 305-307]). In diesem Sinne bezeichnet die rote IS-Kurve im Quadranten (5) der Abbildung 2 den geometrischen Ort aller Gleichgewichte auf dem Gütermarkt.
Die Herleitung der IS-Kurve kann auf zwei Wegen erfolgen. Während die
sogenannte Sparsicht auf die Gleichgewichtsbedingung (4)
rekurriert, bezieht sich die Konsumsicht auf die Gleichung (1).
Im vorliegenden Fall stellt der Quadrant (7) die Gleichgewichtsbedingung
I+G = S+T dar. Die Herleitung der Sparfunktion S(Y) ergibt sich aus
(2) als S = Y−C−T. Unter Berücksichtigung der
Verhaltensgleichungen erhält man
| ||||||||||
Da im Quadranten (8) nicht nur die Sparfunktion, sondern auch die Steuerfunktion enthalten ist, beschreibt die dargestellte Gerade die Beziehung S(Y)+T(Y) = −C0+(1−c(1−t))Y. Man beachte, dass für sehr kleine Einkommen entspart werden muss, um den autonomen Konsum zu decken.
Abschließend wird die IS-Kurve konstruiert. Formal ist die implizite
Gleichung
|
nach dem Zinssatz i aufzulösen. Geometrisch reicht es aus, einen Zinssatz i* vorzugeben. Damit liegt nicht nur die realisierte Investition I(i*), sondern auch I(i*)+G fest. Über die obige Gleichung kann nun S(Y*)+T(Y*) bestimmt werden, womit auch das zugehörige gleichgewichtige Volkseinkommen Y* bekannt ist; die realisierte und die geplante Investition stimmen überein. Das Punktepaar (i*,Y*) ist zwar nicht explizit der Abbildung 1 zu entnehmen, dennoch sollte das Konstruktionsprinzip mit Hilfe der grau eingezeichneten Linien nachvollziehbar sein. Die vollständige IS-Kurve ergibt sich, indem man die geschilderte Ableitung für alle Zinssätze wiederholt.
2.3.2 Konsumsicht
Optional kann die Konsumsicht über das Icon
![]() eingestellt
werden. In diesem Fall dient die 45°-Linie im Quadranten (7) der
Abbildung 2 lediglich der Übertragung des I+G-Wertes aus dem
Quadranten (6) in den Quadranten (8). Dort wird die
Gleichgewichtsbedingung (1) ebenfalls als 45°-Linie angegeben.
Außerdem ist die Kurve I+G+C = I(i)+G+C0+c(1−t)Y abgetragen worden. Gibt man
wiederum den Zinssatz i* vor, so lautet der Ordinatenabschnitt dieser Kurve
I(i*)+G+C0. Die ungeplante Investition ist im Schnittpunkt mit
der Ursprungsgeraden
eingestellt
werden. In diesem Fall dient die 45°-Linie im Quadranten (7) der
Abbildung 2 lediglich der Übertragung des I+G-Wertes aus dem
Quadranten (6) in den Quadranten (8). Dort wird die
Gleichgewichtsbedingung (1) ebenfalls als 45°-Linie angegeben.
Außerdem ist die Kurve I+G+C = I(i)+G+C0+c(1−t)Y abgetragen worden. Gibt man
wiederum den Zinssatz i* vor, so lautet der Ordinatenabschnitt dieser Kurve
I(i*)+G+C0. Die ungeplante Investition ist im Schnittpunkt mit
der Ursprungsgeraden
|
gleich Null und legt das zugehörige gleichgewichtige Volkseinkommen Y* fest. Wie zuvor lässt sich das Konstruktionsprinzip mit Hilfe der grauen Linien verfolgen. Jedes Einkommen Y′ < Y* impliziert, dass die geplanten Ausgaben C+I+G das tatsächliche Einkommen Y′ übersteigen. Der resultierende Nachfrageüberschuss kann nur gedeckt werden, indem die Läger abgebaut werden. Dieser Vorgang entspricht einer (negativen) ungeplanten Investition, wie sie der Abbildung 2 zu entnehmen ist. Das Programm liefert eine entsprechende Grafik, indem man mit der Maus auf einen Punkt im (Y,i)-Diagramm klickt.
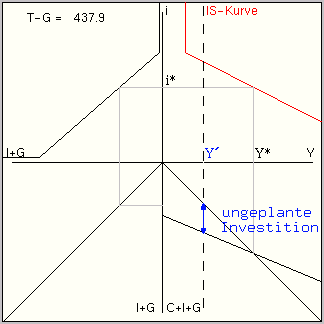 Abbildung 2: Darstellung der ungeplanten Investition in der Konsumsicht
Abbildung 2: Darstellung der ungeplanten Investition in der Konsumsicht
2.3.3 Eigenschaften der IS-Kurve
Programmintern werden sämtliche Kurven analytisch konstruiert und nicht
punktweise hergeleitet. Insbesondere für die IS-Kurve ergibt sich im Bereich
i1 ≤ i ≤ i2:
| ||||||||||||||||||||
Damit verschiebt jede Erhöhung einer autonomen Größe C0, I0 oder der
Instrumentvariablen G die IS-Kurve nach rechts, so wie es vom Programm
bestätigt wird. Man beachte, dass der für die Analyse wichtige
Staatsausgabenmultiplikator
|
in der grafischen Darstellung eine eher untergeordnete Rolle spielt.
Die negative Steigung der IS-Kurve
|
hängt von den Parametern c, t und ρ ab. Ändert man die Konsumquote
oder den Steuersatz via Schieberegler, so stellen sich folgende Effekte ein:
| ||||||||||||||
Mit Hilfe des Programms lässt sich kontrollieren, dass die IS-Kurve flacher
verläuft, wenn die marginale Konsumquote c erhöht wird. Dagegen wird die
Kurve steiler, wenn man den Steuersatz t anhebt. Der Parameter ρ > 0 wird
implizit durch die beiden Knickstellen der Investitionskurve bestimmt.
|
Wenn man also I(i1) erhöht, dann nimmt ρ zu und die IS-Kurve verläuft
flacher, denn
|
3 Das Gleichgewicht auf dem Geldmarkt
3.1 Die Geldnachfrage
Auf dem Geldmarkt der Abbildung 3 werden zwei Kassenhaltungsmotive
unterschieden. Wie in der klassischen Theorie betont die Transaktionskasse 4
LT die Tauschmittelfunktion des Geldes, während die von Keynes hinzugefügte
Spekulationskasse LS die Rolle des Geldes als Vermögensobjekt hervorhebt.
Die mehr oder weniger traditionelle Komponente dieser Keynesschen Theorie der
Liquiditätspräferenz wird im Quadranten (6) dargestellt und
besagt, dass die reale Transaktionskasse proportional vom Einkommen Y
abhängt,5
| (8) |
wobei der Kassenhaltungskoeffizient k > 0 numerisch unter (1) als k = 0,07 vorgegeben ist.
![]() Außer über den Schieberegler kann der Wert für k
auch indirekt mit Hilfe der Maus manipuliert werden, indem man die Kurve im
Quadranten (6) bei gedrückter rechter Maustaste verschiebt.
Außer über den Schieberegler kann der Wert für k
auch indirekt mit Hilfe der Maus manipuliert werden, indem man die Kurve im
Quadranten (6) bei gedrückter rechter Maustaste verschiebt.
Für die zinsabhängige Spekulationskasse im Quadranten (4) wird eine
ähnliche Vorschrift wie für die Investition gewählt:
| (9) |
![]() Analog zur Investitionsfunktion kann auch der Parameter δ > 0 nur
indirekt eingestellt werden, indem man die Knickstellen der LS-Kurve mit
der Maus verändert.
Analog zur Investitionsfunktion kann auch der Parameter δ > 0 nur
indirekt eingestellt werden, indem man die Knickstellen der LS-Kurve mit
der Maus verändert.
|
Der positive Parameter δ besagt, dass die Liquiditätspräferenz für spekulative Zwecke gegenüber Wertpapieren6 zunimmt, wenn der Zinssatz i bei gegebenen Erwartungen über den zukünftigen Zinssatz fällt. Dabei wird die Geldnachfrage vollkommen elastisch, wenn der Zinssatz eine untere Grenze erreicht, d.h. ∂L/∂i→ −∞ für i→ i1′.
Die gesamtwirtschaftliche reale Geldnachfrage L(Y,i) = LT(Y)+LS(i) wird nun dem Geldangebot gegenübergestellt.
3.2 Das Geldangebot
Damit die reale Geldnachfrage mit dem nominalen Geldangebot M verglichen werden kann, muss M durch das an dieser Stelle parametrisch gegebene Preisniveau P dividiert werden. Als Instrument der Geldpolitik lässt sich das nominale Geldangebot M parametrisch unter (2) verändern.
![]() Der Startwert M = 110 kann auch hier indirekt manipuliert werden, indem man die
Kurve im Quadranten (5) bei gedrückter rechter Maustaste verschiebt. An
dieser Stelle bleibt der Geld- und Kreditschöpfungsmechanismus unbeachtet, so
dass insbesondere von einer Steuerung der Geldmenge mit Hilfe eines
Mindestreservesatzes abgesehen werden muss.
Der Startwert M = 110 kann auch hier indirekt manipuliert werden, indem man die
Kurve im Quadranten (5) bei gedrückter rechter Maustaste verschiebt. An
dieser Stelle bleibt der Geld- und Kreditschöpfungsmechanismus unbeachtet, so
dass insbesondere von einer Steuerung der Geldmenge mit Hilfe eines
Mindestreservesatzes abgesehen werden muss.
3.3 Die Bestimmung des Gleichgewichts
3.3.1 Die Ableitung der LM-Kurve
Analog zum Gütermarkt lässt sich nun die LM-Kurve
als geometrischer Ort aller
Gleichgewichte auf dem Geldmarkt herleiten. Zu diesem Zweck enthält der
Quadrant (5) die Gleichgewichtsbedingung
| (10) |
Unter formalen Gesichtspunkten ergibt sich die grüne LM-Kurve im Quadranten (3), indem man die Verhaltensgleichungen für die Transaktionskasse und die Spekulationskasse einsetzt und nach dem Zinssatz auflöst. Aus geometrischer Sicht wird wie zuvor ein Zinssatz i* vorgegeben. Damit ist LS = LS(i*) bekannt, so dass sich LT = M/P−LS bestimmen lässt. Nun kann über LT = LT(Y*) das zugehörige gleichgewichtige Einkommen Y* angegeben werden. Dieses Konstruktionsprinzip wird durch die grauen Linien veranschaulicht und liefert den ersten Punkt (i*,Y*) auf der LM-Kurve .
3.3.2 Eigenschaften der LM-Kurve
Der Verlauf der LM-Kurve
im Bereich i1′ ≤ i ≤ i2′ ergibt sich aus
| (11) |
Ohne diese Gleichung nach dem Zinssatz aufzulösen, kann die (positive)
Steigung der LM-Kurve
über den Satz der impliziten Differentiation angegeben
werden,
|
Die Steigung nimmt zu, wenn der Parameter k erhöht oder wenn δ gesenkt wird. Analog verschiebt eine Ausweitung der Geldmenge M die LM-Kurve nach rechts, während eine Erhöhung des Preisniveaus die LM-Kurve nach links schiebt. Auch hier können die Ergebnisse direkt kontrolliert werden, indem man die entsprechenden Variablen mit der Maus ändert. Wird beispielsweise im Quadranten (6) die rechte Maustaste festgehalten, so lässt sich die Steigung der LT-Kurve, also k, unmittelbar variieren. Die entsprechenden Effekte auf die LM-Kurve werden simultan angezeigt.
3.3.3 Der klassische Bereich der LM-Kurve
Im Fall i2′ < i gibt es keine Spekulationskasse, d.h. LS(i) = 0, und
Geld wird nur noch zu Transaktionszwecken nachgefragt, M/P = LT(Y). Die
resultierende Beziehung M = k P Y wird zu Ehren von Marshall und Pigou als
Cambridge-Gleichung bezeichnet. Sie besagt zunächst nichts anderes, als
dass die Geldmenge M benötigt wird, um bei der durchschnittlichen
Kassenhaltungsdauer k das nominale Volkseinkommen P Y umzusetzen.
Definiert man nun die Umschlagshäufigkeit des Geldes v als Kehrwert der
Kassenhaltungsdauer v = 1/k, so ergibt sich die Quantitätsgleichung
bzw. Fishersche Verkehrsgleichung
|
Unter der Annahme, dass die Umschlagshäufigkeit konstant ist,
v = v resultiert die Quantitätstheorie
M v = P Y. Wenn also das reale Einkommen angebotsseitig festliegt (Y = konst.), dann ist das Preisniveau eine Funktion der nominalen Geldmenge, P = f(M). Daher wird der zugehörige vertikale Bereich der LM-Kurve häufig als klassischer Bereich bezeichnet.
Auf den von Keynes betonten Fall einer vollkommen elastischen Geldnachfrage mit ∂L/∂i→ −∞ wird später genauer eingegangen. Im Gegensatz zum klassischen - also vertikalen - Bereich handelt es sich hierbei um den horizontalen Bereich der LM-Kurve .
4 Die gesamtwirtschaftliche Endnachfrage
4.1 Das simultane Gleichgewicht auf dem Güter- und Geldmarkt
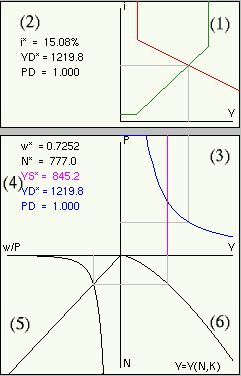 Abbildung 4: Gesamtwirtschaftlicher Nachfrageüberschuss in einer geschlossenen
Volkswirtschaft
Abbildung 4: Gesamtwirtschaftlicher Nachfrageüberschuss in einer geschlossenen
Volkswirtschaft
Die zuvor abgeleitete IS-Kurve (7) und die LM-Kurve (11) werden nun in ein gemeinsames (Y,i)-Diagramm übertragen, das dem oberen Teil (1) der Abbildung 4 zu entnehmen ist. Im Schnittpunkt der roten IS-Kurve mit der grünen LM-Kurve stellt sich ein simultanes Gleichgewicht ein, bei dem sowohl der Gütermarkt als auch der Geldmarkt für das gegebene Preisniveau P ausgeglichen sind. Die zugehörigen numerischen Werte i* und YD* sind dem Feld (2) zu entnehmen, wobei auch das zugrundeliegende Preisniveau PD ausgewiesen wird. Auch die grauen Hilfslinien beziehen sich auf dieses Gleichgewicht.
![]() Für eine geschlossene Volkswirtschaft kann die Stabilität des
IS-LM-Gleichgewichts getestet werden, indem man mit der Maus einen
Startpunkt im (Y,i)-Diagramm (1) antippt.
Für eine geschlossene Volkswirtschaft kann die Stabilität des
IS-LM-Gleichgewichts getestet werden, indem man mit der Maus einen
Startpunkt im (Y,i)-Diagramm (1) antippt.
Der implementierte
Algorithmus berechnet dann einen Zeitpfad, der ähnlich zu
Otruba, Munduch, Stiassny (1996,S. 183]veranschaulicht, wie das System nach einer Störung in
sein Gleichgewicht zurückfindet. Die Idee des Anpassungsmechanismus basiert
auf zwei Beobachtungen. Erstens sind Punkte unterhalb der LM-Kurve bei dem
gegebenen Einkommen Y mit einer Überschussnachfrage nach Geld verbunden,
LS(i) > M/P−kY. Da das reale Geldangebot M/P fixiert ist, kann die
Überschussnachfrage nur durch einen entsprechenden Verkauf von Wertpapieren
gedeckt werden. Der resultierende Angebotsüberschuss auf dem Wertpapiermarkt7
lässt die Wertpapierkurse fallen, so dass der Zinssatz i steigt, bis der
Geldmarkt wieder im Gleichgewicht ist. Analog implizieren Punkte oberhalb der
LM-Kurve, dass der Zinssatz fällt.
Zweitens bedeuten Punkte rechts der IS-Kurve bei dem gegebenen Zinssatz i, dass die erwartete Nachfrage Y = C+S+T größer als die tatsächliche Nachfrage Y = C+I+G ist. Der ungeplante Lageraufbau impliziert eine Kontraktion des Einkommens, so wie das Einkommen bei einem ungeplanten Lagerabbau expandiert.
Bis auf diesen Anpassungsmechanismus basieren alle Berechnungen des Programms auf der Annahme, dass das simultane IS-LM-Gleichgewicht stets eingehalten wird. Weder auf dem Geldmarkt noch auf dem Gütermarkt treten ungeplante Größen auf.
4.2 Ableitung der gesamtwirtschaftlichen Endnachfrage
Bis zu diesem Zeitpunkt ist das Preisniveau P als exogene Variable behandelt
worden, wobei zu Beginn8
P = 1 gilt. Wenn man jedoch ein neues Preisniveau einstellt, so
fällt unmittelbar auf, dass mit P auch das IS-LM-Gleichgewicht (Y*,i*)
variiert. Unter Vernachlässigung des Zinssatzes wird jedem Preisniveau P ein
gleichgewichtiges Einkommen zugeordnet, das von der Nachfrageseite her
bestimmt ist und daher mit YD bezeichnet wird. Die zugehörige geometrische
Beziehung entspricht der blauen Kurve im Quadranten (3) der
Abbildung 4. Analytisch wird diese Kurve hergeleitet, indem man
das simultane Gleichgewicht auf dem Gütermarkt - also die IS-Kurve
(7) - und dem Geldmarkt - also die LM-Kurve
(11) - nach
dem Preisniveau auflöst:
|
Bereits im vorliegenden extrem einfachen Beispiel wird es schwierig, aus dieser Beziehung die explizite gesamtwirtschaftliche Nachfrage YD als Funktion von P zu bestimmen. Schon einfache Änderungen der marginalen Konsumquote c zeigen, wie vielfältig sich die Nachfragekurve verändert und wie viele Sonderfälle zu beachten sind. Allerdings müssen Variationen des Preisniveaus stets dazu führen, dass das angezeigte Gleichgewicht auf der unveränderten blauen Kurve entlang wandert.
5 Das gesamtwirtschaftliche Angebot
5.1 Der Produktionssektor
Der nächste Schritt besteht darin, die zuvor abgeleitete Nachfrage
YD = YD(P) um ein entsprechendes Angebot YS zu ergänzen. Zu diesem Zweck
wird im Quadranten (6) der Abbildung 4 eine
gesamtwirtschaftliche Produktionsfunktion Y = Y(N,K) eingeführt. Für das
Programm ist eine linear-homogene Cobb-Douglas-Funktion
| (12) |
gewählt worden, wobei der Kapitalstock zunächst als konstant unterstellt wird, K = Kkonst.
![]() Der zugehörige Schieberegler in der Abbildung 9 zeigt, dass der
Kapitalstock zu Beginn auf K = 1000 festgelegt worden ist. Auch dieser Wert
kann manipuliert werden, indem man bei gedrückter rechter Maustaste den
Grafen der Produktionsfunktion verschiebt. Der Exponent des Kapitalstocks hat
den Wert alpha = a = 0,3333. Abschließend lässt sich die
nachgefragte Menge des Faktors Arbeit ND über die notwendige Bedingung der
Gewinnmaximierung von der Inputseite bestimmen,
Der zugehörige Schieberegler in der Abbildung 9 zeigt, dass der
Kapitalstock zu Beginn auf K = 1000 festgelegt worden ist. Auch dieser Wert
kann manipuliert werden, indem man bei gedrückter rechter Maustaste den
Grafen der Produktionsfunktion verschiebt. Der Exponent des Kapitalstocks hat
den Wert alpha = a = 0,3333. Abschließend lässt sich die
nachgefragte Menge des Faktors Arbeit ND über die notwendige Bedingung der
Gewinnmaximierung von der Inputseite bestimmen,
| (13) |
Darin wird angenommen, dass der Nominallohnsatz w sowie das Preisniveau P
aus Sicht des Produktionssektors gegeben sind. Löst man diese Gleichung
unter Beachtung der Cobb-Douglas-Funktion nach N auf, so resultiert die
hyperbelartige Nachfragekurve im Quadranten (5) der
Abbildung 4. Man beachte an dieser Stelle, dass nach dem
Euler-Theorem
|
kein positiver gesamtwirtschaftlicher Gewinn erzielt wird, d.h. P Y−w N−i PK K = 0, sofern der reale Zinssatz i mit der Grenzleistungsfähigkeit des Kapitals (P/PK)∂Y/∂K übereinstimmt. Insofern stimmen die realen Erlöse Y mit den Faktorkosten überein, die sich aus den Löhnen wN/P und den Kapitalkosten iPKK/P zusammensetzen. Wie im Einkommenskonto (2) angedeutet worden ist, stimmt die reale Faktorentlohnung in der Tat mit dem realen Volkseinkommen überein.
5.2 Der Arbeitsmarkt
![]() Auf dem Arbeitsmarkt werden der Reallohnsatz w/P und die Beschäftigung N
bestimmt. Die Arbeitsnachfrage ND des Produktionssektors ist bereits
hergeleitet worden. Damit fehlt eine letzte Verhaltensgleichung für das
Arbeitsangebot NS. Die unterstellte Ursprungsgerade im Quadranten (5)
Auf dem Arbeitsmarkt werden der Reallohnsatz w/P und die Beschäftigung N
bestimmt. Die Arbeitsnachfrage ND des Produktionssektors ist bereits
hergeleitet worden. Damit fehlt eine letzte Verhaltensgleichung für das
Arbeitsangebot NS. Die unterstellte Ursprungsgerade im Quadranten (5)
| (14) |
besagt nichts Anderes, als dass das Arbeitsangebot mit steigendem Reallohnsatz zunimmt; die Kurve kann bei gedrückter rechter Maustaste verschoben werden. Die Herleitung einer solchen Angebotsfunktion findet man in Otruba, Munduch, Stiassny (1996,S. 115 ff.]. Das zugehörige Problem der Nutzenmaximierung geht davon aus, dass der Nutzen eine Funktion des realen Konsums C und der Freizeit F ist. Dabei ist zum einen die Zeitrestriktion NS+F = 1 zu beachten, wobei die Periodenlänge auf Eins normiert worden ist. Zum anderen darf der Konsum C das real verfügbare Einkommen Yv = (1−t)Y mit Y = (iPKK+wNS)/P nicht übersteigen. Man beachte, dass das intertemporale Entscheidungsproblem hier zur Vereinfachung vernachlässigt worden ist. Denn das verfügbare Einkommen Yv muss nicht nur den heutigen Konsum C, sondern auch den zukünftigen Konsum über die Ersparnis S abdecken,9 so wie es die Budgetrestriktion (2) verlangt, C+S = (1−t)Y.
Auf einem funktionsfähigen Arbeitsmarkt wird sich ein Gleichgewicht einstellen
und zwar dort, wo Angebot NS und Nachfrage ND übereinstimmen,
| (15) |
Sofern alles, was produziert wird, auch angeboten wird, ergibt sich die
magentafarbene Angebotsfunktion im Quadranten (3),
YS = Y(N,Kkonst).
Man beachte, dass diese vertikale Kurve nicht vom Preisniveau beeinflusst
wird, weil sich der Nominallohnsatz w immer so an das Preisniveau P
anpasst, dass derselbe Reallohnsatz (w/P)fix resultiert. Damit das
gesamtwirtschaftliche Angebot und die gesamtwirtschafliche Nachfrage im
Einklang stehen,
| (16) |
muss sich ein adäquates Preisniveau einstellen, womit gleichzeitig der Geldlohnsatz w determiniert ist.
6 Das gesamtwirtschaftliche Gleichgewicht
6.1 Die Lösung des Modells
6.1.1 Formale Aspekte des interdependenten Gleichungssystems
Mit dem Arbeitsmarkt ist der letzte Teilmarkt vorgestellt worden, der für die Ableitung des gesamtwirtschaftlichen Gleichgewichts benötigt wird. Damit stehen neun Gleichungen zur Verfügung, nämlich (1), (5), (6), (8), (9), (10), (12), 2×(15), mit deren Hilfe sich potentiell die neun Variablen Y, i, C, I, LS, LT, P, N und w/P bestimmen lassen. Sofern man sich auf die fünf wesentlichen Variablen Y, i, P, N, w/P konzentriert, reicht es aus, die fünf Gleichungen: (7), (11), (12), 2×(15) heranzuziehen. Gleichzeitig können zwei Instrumente eingesetzt werden, um das Gleichgewicht von außen zu beeinflussen, nämlich die Staatsausgaben G und das nominale Geldangebot M.
Die Lösung des interdependenten Gleichungssystems beginnt wie in Böckmann, Rettig (1998) mit einem funktionsfähigen Arbeitsmarkt, so dass sich der gleichgewichtige Reallohnsatz (w/P)* unabhängig vom Preisniveau dort einstellt, wo Vollbeschäftigung N* = NS = ND herrscht. Da das Angebot nicht vom Preisniveau abhängt, lautet das Vollbeschäftigungseinkommen, Y* = Y(N*,Kkonst). Also resultiert das gleichgewichtige Preisniveau P* aus Y* = YD(P). Damit liegt via M/P* = L(Y*,i) auch der Zinssatz i* fest. Schließlich lassen sich der Konsum und die Investition bestimmen.
6.1.2 Der Preismechanismus
Nachdem das Programm gestartet worden ist, wird der Anwender folgendes Problem
feststellen. Einerseits wird für den Gütermarkt und den Geldmarkt zwar ein
simultanes Gleichgewicht ausgewiesen, andererseits befindet sich auch der
Arbeitsmarkt im Gleichgewicht. Dennoch besteht bei dem unterstellten
Preisniveau P = 1 ein Nachfrageüberschuss, YD > YS. Um dieses
Problem zu beseitigen10,
kann das Preisniveau entweder per Schieberegler erhöht werden oder über das
Icon
![]() angepasst werden. Im letzten Fall wird ein
beobachtbarer Preismechanismus ausgelöst, der P so lange erhöht,
wie YD > YS gilt et vice versa. In fast allen getesteten Fällen
reicht der implementierte Mechanismus aus, ein nahezu exaktes Gleichgewicht
auf sämtlichen Märkten herzustellen.
angepasst werden. Im letzten Fall wird ein
beobachtbarer Preismechanismus ausgelöst, der P so lange erhöht,
wie YD > YS gilt et vice versa. In fast allen getesteten Fällen
reicht der implementierte Mechanismus aus, ein nahezu exaktes Gleichgewicht
auf sämtlichen Märkten herzustellen.
6.2 Das Walras-Gesetz
In den bisherigen Ausführungen fällt auf, dass die Produktionsfunktion
(12) zwar die eingesetzte (also nachgefragte) Menge des Faktors
Kapital enthält, dass dieser Nachfrage jedoch kein entsprechendes Angebot
gegenübersteht. Diese Lücke wird geschlossen, indem man die Grundgleichung
der Vermögensrechnung für den Sektor der privaten Haushalte heranzieht;
vgl. Stobbe (1994,S. 69 f.]. Um keinen zusätzlichen Markt für physische
Kapitalgüter einführen zu müssen, wird unterstellt, dass die Unternehmen ihre
gesamten Investitionen über Aktienemissionen finanzieren. Der Aktienwert V
beschreibt damit das monetäre Äquivalent des Kapitalstocks K (Sachvermögen
der Unternehmen) und nur die Haushalte fragen Aktien nach.11
Im vorliegenden Fall besteht das nominale Vermögen P W der Haushalte aus
drei verschiedenen nominalen Forderungen: (1) der Aktienwert V als
Forderung gegenüber den Unternehmen, (2) die Geldmenge M als Forderung
gegenüber der Zentralbank und (3) die Forderungen gegenüber dem Staat B,
wobei B den Wert der Schuldverschreibungen bezeichnet, die der Staat etwa zur
Finanzierung seiner Budgetdefizite ausgibt.
| (17) |
Das Pendant dieser Bestandsgleichung liefert das Vermögensänderungskonto
des privaten Sektor I = S, wobei I = δK = δV die Änderung des
Sachvermögens und S = δ(PW) die Änderung des Reinvermögens angibt. Für
die Bilanzgleichung (17) ist nun die gewünschte Aufteilung des
Vermögens12
in V+B und M herzuleiten (Sargent (1994,S. 14 f.]). Das optimale
Portfolio stellt sich entsprechend der beiden Nachfragefunktionen
(VD+BD)/P = b(Y,i,W) und MD/P = L(Y,i) ein, wobei für die Geldnachfrage
unterstellt worden ist, dass sie nicht vom realen Vermögen W abhängt.
Solange die privaten Haushalte ihre Bilanzrestriktion einhalten und der
Geldmarkt im Gleichgewicht ist M/P = L(Y*,i*), muss auch
|
erfüllt sein. Dieses Aussage entspricht dem Walras-Gesetz. Befinden sich drei der vier Märkte (Geld-, Güter-, Arbeits-, Wertpapiermarkt13) im Gleichgewicht und sind alle Budgetgleichungen erfüllt, dann ist auch der vierte Markt ausgeglichen.
Die klassische Sicht kann das Programm zur Zeit nicht darstellen. Auch dort wird die vertikale gesamtwirtschaftliche Angebotskurve Y* = YS aus einem funktionsfähigen Arbeitsmarkt abgeleitet, dessen Gleichgewicht durch (w/P)* und N* gekennzeichnet ist. Mit Hilfe der Quantitätstheorie Mv = PY*ist damit das Preisniveau P* determiniert.
Während im Programm von einer Konsumfunktion C(Yv) mit residualer Ersparnis S ausgegangen wird, unterstellt die Klassik die Gleichgewichtsbedingung S(i) = I(i), d.h., das reale Angebot und die reale Nachfrage auf dem Kapitalmarkt bestimmen den Zinssatz i*. Residual wird das Gleichgewicht auf dem Gütermarkt YD = C+I(i*) hergestellt, indem man annimmt, dass sich jedes Angebot YS selbst seine Nachfrage YD schafft, so wie es das Saysche Theorem14 postuliert: C* = Y*−I(i*).
Schließlich ist die Dichotomie von realen und monetären Größen einer Volkswirtschaft als Resultat der Quantitätstheorie zu betonen. Demnach ist die reale Sphäre (N*, Y*, i*, (w/P)*) unabhängig von den nominalen Variablen P* und w*. Eine Erhöhung der Geldmenge hat keine Auswirkung auf die realen Größen und bewirkt lediglich einen Preisanstieg, wobei neben P auch der Geldlohnsatz w steigt.
6.3 Die Keynes-Fälle
6.3.1 Die Liquiditätsfalle
Die Abbildung 5 zeigt eine sogenannte button group, mit deren Hilfe sich bestimmte Szenarien einstellen lassen, die aus der Keynesschen Analyse bekannt geworden sind.
 Abbildung 5: Wahl einiger Spezialfälle
Abbildung 5: Wahl einiger Spezialfälle
In der Liquiditätsfalle wird eine vollkommen zinselastische Geldnachfrage unterstellt, d.h. ∂L/∂i = ∂LS/∂i = −∞. Mit Blick auf den Geldmarkt handelt es sich demnach um den horizontalen Bereich der LM-Kurve. Die weitere Analyse zeigt, dass die gesamtwirtschaftliche Nachfragekurve YD an der Stelle des IS-LM-Gleichgewichts senkrecht verläuft. Der unterstellte Nachfragemangel spiegelt sich in einer Unterbeschäftigung wider, deren Umfang im Beispiel nicht besonders umfangreich ausfällt. Entscheident ist vielmehr, dass der Preismechanismus nicht in der Lage ist, die Arbeitslosigkeit zu beseitigen. Die vollkommene Unwirksamkeit der Geldpolitik und die hohe Wirksamkeit der Fiskalpolitik können nun über die Veränderungen der Geldmenge M bzw. der Staatsausgaben G vorgeführt werden.
6.3.2 Die Investitionsfalle
Im zweiten Fall wird auf dem Gütermarkt eine vollkommen zinsunelastische Investitionsnachfrage angenommen, d.h. ∂I/∂i = 0. In diesem Bereich verläuft die IS-Kurve senkrecht. Auch hier resultiert eine gesamtwirtschaftliche Nachfragekurve YD, deren absolute Steigung im relevanten Bereich unendlich groß wird, ∂YD/∂P = −∞. Der gesamtwirtschaftliche Nachfragemangel mündet in der Arbeitslosigkeit, die wie zuvor auf dem Arbeitsmarkt rot dargestellt wird. Prinzipiell kann der Preismechanismus die Arbeitslosigkeit überwinden. Wenn das Preisniveau jedoch nicht beliebig reduziert werden kann, dann lässt sich die Effizienz wirtschaftspolitischer Maßnahmen über entsprechende Änderungen der beiden Instrumentvariablen demonstrieren.
6.3.3 Nach unten starre Geldlohnsätze
Wird ein minimaler Geldlohnsatz wmin > 0 über
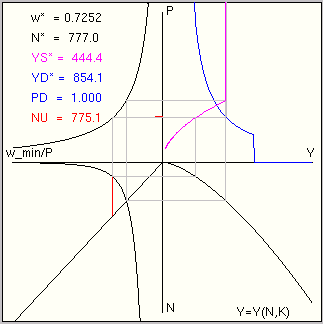 Abbildung 6: Nach unten starrer Geldlohnsatz
Abbildung 6: Nach unten starrer Geldlohnsatz
den entsprechenden Schieberegler w_min eingestellt, so springt das Programm automatisch in eine Routine, die prüft, ob der Minimallohnsatz bei dem gegebenen Preisniveau den gleichgewichtigen Lohnsatz übersteigt. In diesem Fall wird die resultierende Unterbeschäftigung ausgewiesen, so wie es die Abbildung 6 darstellt. Außerdem wird die gesamtwirtschaftliche Angebotsfunktion dahingehend modifiziert, dass bei hohen Reallohnsätzen nicht auf dem Niveau der Vollbeschäftigung produziert wird. Die Hyperbel wmin = (wmin/P) P wird in den entsprechenden Quadranten aufgenommen. Sie wird ausgeblendet sobald der gleichgewichtige Reallohnsatz w/P über wmin/P liegt. Man beachte, dass nun entweder Vollbeschäftigung herrscht oder die Ursache für Arbeitslosigkeit in einem Nachfragemangel zu suchen ist.
Je nach Situation kann der Preismechanismus die Arbeitslosigkeit in der Ausgangssituation vollständig abbauen, indem die zu hohen Reallohnsätze durch Preissteigerungen deflationiert werden. Wenn man jedoch, die Investitionskurve so modifiziert, dass die gesamtwirtschaftliche Nachfragekurve die zugehörige Angebotskurve im ansteigenden Bereich schneidet, dann bleibt ein Teil der Arbeitslosigkeit bestehen. Dieses Problem lässt sich lösen, indem man eine expansive Fiskal- oder Geldpolitik durchführt. Beide Vorgehensweisen, lösen de facto einen Inflationsprozess aus, der den zu hohen Reallohnsatz entwertet.
Der ungewöhnliche konvexe Verlauf der gesamtwirtschaftlichen Angebotskurve verschwindet, wenn man den Parameter a auf einen Wert größer als 0,5 einstellt. Da jedoch in dem Modell davon ausgegangen wird, dass die beiden Produktionsfaktoren entsprechend ihrer monetären Grenzproduktivität entlohnt werden und dass die Produktionsfunktion linearhomogen ist, sollten die Kapitalertragsquote a und die Lohnquote b realistischerweise Werte um a = 1/3 und b = 2/3 annehmen.
7 Erweiterungen
7.1 Die offene Volkswirtschaft
7.1.1 Das modifizierte Kontensystem
Über das Icon
![]() kann eine offene Volkswirtschaft eingestellt
werden. Nur in diesem Fall ist der Schieberegler für den Wechselkurs e
wirksam. Wie die Abbildung 9 zeigt, wird zunächst e = 0,6
unterstellt.
kann eine offene Volkswirtschaft eingestellt
werden. Nur in diesem Fall ist der Schieberegler für den Wechselkurs e
wirksam. Wie die Abbildung 9 zeigt, wird zunächst e = 0,6
unterstellt.
Im Hinblick auf die Ableitung der ex post Identität (22)
sind nun die ökonomischen Transaktionen zwischen dem Inland und dem
Ausland auf dem Gütermarkt zu berücksichtigen. Das modifizierte Kontensystem
(1)-(3) lautet
| ||||||||||||
Die Gegenbuchung für den Exportwert Ex und den Importwert Im im
Produktionskonto (18) sowie den Kapitalexport KEx und den
Kapitalimport KIm im Finanzierungskonto (20) werden
im Konto der übrigen Welt vorgenommen, das aus Sicht des Inlands
aufgeschrieben wird.
| (21) |
Darin wird Z häufig als Saldo der Zahlungsbilanz bezeichnet, obwohl man
korrekt vom Saldo des Devisenbilanzkontos sprechen müsste. Ist die
Zahlungsbilanz in dem Sinne ausgeglichen, dass Z = 0 vorliegt, dann erhält man
aus Ex−Im = KEx−KIm. Nun liefert (20) die ex post
Identität einer offenen Volkswirtschaft mit staatlicher Aktivität in der Form
| (22) |
wobei die Staatsausgaben G = ISt+CSt und die Steuereinnahmen T = CSt+SSt zu berücksichtigen sind.
7.1.2 Der modifizierte Gütermarkt
Für den Außenbeitrag Ex−Im wird nun angenommen, dass er vom heimischen Einkommen und vom heimischen Preisniveau abhängt. Darüber hinaus wird er vom Wechselkurs beeinflusst. Welcher genaue Zusammenhang vorausgesetzt wird, ist Gegenstand des nächsten Abschnitts. Gleichzeitig sind die Nettokapitalimport KIm−KEx eine Funktion des heimischen Zinssatzes. Die entsprechenden ausländischen Größen werden als konstant unterstellt. Damit kann auf dem Gütermarkt die (hellblaue) Kurve eingezeichnet werden, die den geometrischen Ort aller außenwirtschaftlichen Gleichgewichte mit Z = 0 angibt. Diese Kurve geht zunächst von einem parametrisch gegebenen Preisniveau und einem gegebenen Wechselkurs aus. Die Punkte oberhalb der Kurve implizieren einen Überschuss in der Zahlungsbilanz, die Punkte unterhalb der Kurve führen zu einem Defizit. Der jeweilige numerische Wert des Saldos wird entsprechend der Abbildung 8 neben dem IS-LM-System ausgewiesen und bezieht sich auf den Schnittpunkt der IS-Kurve mit der LM-Kurve.
7.1.3 Die Weltmärkte
Die Herleitung der Z = 0-Kurve besteht aus
drei Teilen: (1) dem Exportwert, (2) dem Importwert und (3) den
Nettokapitalimporten. Um das Modell einfach zu halten, wird für die
Nettokapitalimporte eine Verhaltensgleichung unterstellt
|
die besagt, dass netto Kapital importiert wird, sofern der heimische Zinssatz i den ausländischen Zinssatz i* übersteigt et vice versa.15
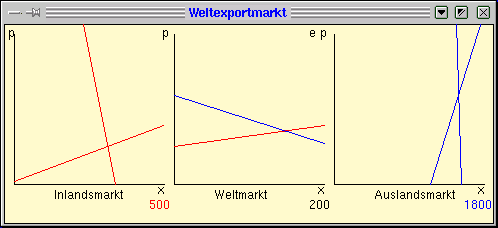 Abbildung 7: Der Weltexportmarkt (Man beachte die unterschiedliche
Skalierung der Gütermenge x.)
Abbildung 7: Der Weltexportmarkt (Man beachte die unterschiedliche
Skalierung der Gütermenge x.)
Die Ableitung des Exportwertes Ex erfolgt anhand des Weltexportmarktes für
ein Gut x mit dem Preis p. Die Nachfrage x1D und das Angebot
x1S im Inland (Land 1) lauten
|
Beide Kurven sind auf dem Inlandsmarkt der Abbildung 7 abgetragen.
Das resultierende Exportangebot x1S−x1D ist dem zugehörigen Weltmarkt zu entnehmen. Für das annahmegemäß 3,6 mal größere Ausland (Land 2) werden analoge Angebots- und Nachfragekurven vorgegeben, wobei die Wahl der Parameter sicherstellen muss, dass der ausländische Autarkiepreis größer als im Inland ist. Andernfalls würde das Gut nicht exportiert. Die fallende Exportnachfrage x2D−x2S wird wiederum auf den Weltmarkt übertragen. Das Gleichgewicht auf dem Weltmarkt determiniert die Exportmenge x* neben dem Weltmarktpreis p1* = e p2*, so dass der Exportwert Ex = p1*x* beträgt. Nun lässt sich veranschaulichen, dass Abwertungen (e steigt) stets den Exportwert vergrößern und die Z = 0-Kurve nach unten verschieben. Dagegen ist der Einfluss heimischer Inflation auf den Exportwert unbestimmt, während sich die Z = 0-Kurve nun nach oben schiebt.
Auf die analoge Herleitung des Weltimportmarktes wird verzichtet. Die einzige Schwierigkeit besteht darin, geeignete Parameterwerte vorzugeben, so dass der Autarkiepreis im Inland höher als im Ausland ist. Gleichzeitig sollte der Importwert in der Größenordnung des Exportwertes liegen.
7.1.4 Mechanismen zum Ausgleich der Zahlungsbilanz
Nachdem die Volkswirtschaft für den Handel geöffnet worden ist, wird in der Regel kein außenwirtschaftliches Gleichgewicht vorliegen, d.h. Z ≠ 0.
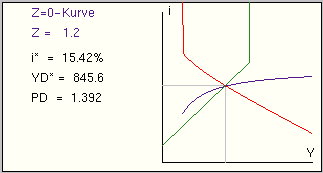 Abbildung 8: Simultanes Gleichgewicht in einer offenen Volkswirtschaft
Abbildung 8: Simultanes Gleichgewicht in einer offenen Volkswirtschaft
Eine Möglichkeit, diesen Saldo zu beseitigen, besteht darin, den Wechselkurs
freizugeben. Ob dieser Weg erfolgreich ist, hängt unter anderem von der
sogenannten Robinson-Bedingung ab, die in Siebert (1994,S. 230 ff.]
diskutiert wird. Die hier umgesetzte Idee des Wechselkursmechanismus ist
einfach, denn Z bezeichnet nichts anderes als das bewertete
Überschussangebot am Devisenmarkt, wobei der Wechselkurs den Preis einer
ausländischen Währungseinheit angibt. Im Fall Z > 0 herrscht also ein
Überschussangebot an Devisen, so dass e fällt und umgekehrt. Wenn nun der
Außenbeitrag Ex−Im so auf die Wechselkursänderung reagiert, dass stets
dZ/de > 0 erfüllt ist, dann wird dieser Mechanismus schließlich Z = 0
sicherstellen. Über das Icon
![]() wird ein entsprechender Prozess
in Gang gesetzt, der den Wechselkurs e erhöht, wenn Z < 0 festgestellt
worden ist et vice versa. Leider schießt das Ergebnis über das Ziel hinaus.
Beispielsweise wird ein Defizit in der Regel in einen Überschuss
verwandelt. Da nun der Wechselkurs in die umgekehrte Richtung korrigiert
werden muss, gleichzeitig aber das Kriterium überprüft wird, ob dZ/de > 0
vorliegt, bricht die Anpassung ab. Nach einigen Aufrufen sollte sich jedoch
das gewünschte Ergebnis der Abbildung 8 einstellen.
wird ein entsprechender Prozess
in Gang gesetzt, der den Wechselkurs e erhöht, wenn Z < 0 festgestellt
worden ist et vice versa. Leider schießt das Ergebnis über das Ziel hinaus.
Beispielsweise wird ein Defizit in der Regel in einen Überschuss
verwandelt. Da nun der Wechselkurs in die umgekehrte Richtung korrigiert
werden muss, gleichzeitig aber das Kriterium überprüft wird, ob dZ/de > 0
vorliegt, bricht die Anpassung ab. Nach einigen Aufrufen sollte sich jedoch
das gewünschte Ergebnis der Abbildung 8 einstellen.
Das Icon
![]() setzt den Geldmengen-Preis-Mechanismus in Gang.
Dabei wird ein fixer Wechselkurs unterstellt, den die Zentralbank stützt,
indem sie die Salden der Zahlungsbilanz ausgleicht. Damit ist gemeint, dass
die Zentralbank im Fall Z > 0 das entsprechende Überschussangebot am
Devisenmarkt gegen eigene Währung aufkauft. Also steigt die Geldmenge im
Umfang dM = Z > 0. Analog gibt die Zentralbank im Fall Z < 0 Devisen ab und
verringert damit das eigene Geldangebot, dM = Z < 0. Simultan zu diesem
Vorgehen sind die zugehörigen endogenen Effekte des Preismechanismus zu
berechnen, denn in der Regel wird eine Ausweitung der Geldmenge
preissteigernde Impulse mit sich bringen und umgekehrt. Auch dieser
Ausgleichsmechanismus liefert ein simultanes innen- und außenwirtschaftliches
Gleichgewicht, wie es in der Abbildung 8 dargestellt ist.
setzt den Geldmengen-Preis-Mechanismus in Gang.
Dabei wird ein fixer Wechselkurs unterstellt, den die Zentralbank stützt,
indem sie die Salden der Zahlungsbilanz ausgleicht. Damit ist gemeint, dass
die Zentralbank im Fall Z > 0 das entsprechende Überschussangebot am
Devisenmarkt gegen eigene Währung aufkauft. Also steigt die Geldmenge im
Umfang dM = Z > 0. Analog gibt die Zentralbank im Fall Z < 0 Devisen ab und
verringert damit das eigene Geldangebot, dM = Z < 0. Simultan zu diesem
Vorgehen sind die zugehörigen endogenen Effekte des Preismechanismus zu
berechnen, denn in der Regel wird eine Ausweitung der Geldmenge
preissteigernde Impulse mit sich bringen und umgekehrt. Auch dieser
Ausgleichsmechanismus liefert ein simultanes innen- und außenwirtschaftliches
Gleichgewicht, wie es in der Abbildung 8 dargestellt ist.
Der Einkommensmechanismus, setzt zunächst ein Festpreismodell voraus, das über
das Icon
![]() eingeschaltet wird. Im Sinne der Multiplikatortheorie
kann eine Änderung der autonomen Exporte nur dann einen Einkommenseffekt
hervorrufen, wenn man von einer Situation mit Unterbeschäftigung ausgeht. Im
Standardfall lässt sich diese Situation am einfachsten über einen
Kapitalstock in der Höhe K = 4500 herstellen, wobei die resultierende
Arbeitslosigkeit auf dem Arbeitsmarkt abzulesen ist. Jeder Klick auf das Icon
eingeschaltet wird. Im Sinne der Multiplikatortheorie
kann eine Änderung der autonomen Exporte nur dann einen Einkommenseffekt
hervorrufen, wenn man von einer Situation mit Unterbeschäftigung ausgeht. Im
Standardfall lässt sich diese Situation am einfachsten über einen
Kapitalstock in der Höhe K = 4500 herstellen, wobei die resultierende
Arbeitslosigkeit auf dem Arbeitsmarkt abzulesen ist. Jeder Klick auf das Icon
![]() löst nun entsprechend dem Saldo der Zahlungsbilanz eine Änderung
der autonomen Exporte aus. Dabei wird der Einfachheit halber unterstellt, dass
ein bestimmter Anteil des Exportwertes den autonomen Exporten entspricht.
Demnach müssen lediglich die Kurven auf dem heimischen Exportmarkt
vertikal verschoben werden. Dem Einkommensmechanismus sind damit enge Grenzen
gesetzt, zumal die Zahlungsbilanz nicht unerheblich von den
Nettokapitalimporten beeinflusst wird.
löst nun entsprechend dem Saldo der Zahlungsbilanz eine Änderung
der autonomen Exporte aus. Dabei wird der Einfachheit halber unterstellt, dass
ein bestimmter Anteil des Exportwertes den autonomen Exporten entspricht.
Demnach müssen lediglich die Kurven auf dem heimischen Exportmarkt
vertikal verschoben werden. Dem Einkommensmechanismus sind damit enge Grenzen
gesetzt, zumal die Zahlungsbilanz nicht unerheblich von den
Nettokapitalimporten beeinflusst wird.
7.2 Wirtschaftswachstum
Das letzte Icon
![]() löst einen Wachstumsprozess aus, der den
Kapazitätseffekt der Investitionen I = δK berücksichtigt, wobei
Abschreibungen nach wie vor vernachlässigt werden. Der Prozess startet in
einem gesamtwirtschaftlichen Gleichgewicht und beachtet dabei, dass das
Arbeitsangebot bei gleichem Reallohnsatz über die Zeit mit der konstanten Rate
g(NS) = n wächst. Sofern der Reallohnsatz konstant bleibt, verlangt ein
Gleichgewicht auf dem Arbeitsmarkt, dass auch die Arbeitsnachfrage mit der
Rate g(ND) = n wächst. Im Fall der Cobb-Douglas-Produktionsfunktion
(12) muss daher auch das gesamtwirtschaftliche Angebot mit der Rate
n wachsen, denn
löst einen Wachstumsprozess aus, der den
Kapazitätseffekt der Investitionen I = δK berücksichtigt, wobei
Abschreibungen nach wie vor vernachlässigt werden. Der Prozess startet in
einem gesamtwirtschaftlichen Gleichgewicht und beachtet dabei, dass das
Arbeitsangebot bei gleichem Reallohnsatz über die Zeit mit der konstanten Rate
g(NS) = n wächst. Sofern der Reallohnsatz konstant bleibt, verlangt ein
Gleichgewicht auf dem Arbeitsmarkt, dass auch die Arbeitsnachfrage mit der
Rate g(ND) = n wächst. Im Fall der Cobb-Douglas-Produktionsfunktion
(12) muss daher auch das gesamtwirtschaftliche Angebot mit der Rate
n wachsen, denn
|
Da die Produktionsfunktion Y = Ka Nb linear-homogen ist,
a+b = 1, erhält man im Wege der logarithmischen Differentiation
| |||||||||||||||
Der Kapitalstock kann aber nur mit der Rate n zunehmen, wenn auch die
Investition I mit dieser Rate wächst. Nimmt man weiterhin an, dass das
Preisniveau konstant ist, dann muss auch YD mit der Rate n wachsen. Bei
einem konstanten Zinssatz muss das Geldangebot dem folgenden Zeitpfad angepasst
werden:
|
Alles, was zu tun bleibt, um den konstanten Zinssatz sicherzustellen, ist, die Staatsausgaben G und den autonomen Konsum C0 mit der Wachstumsrate n zu versehen. Dieses Vorgehen ist nicht unplausibel, wenn man die zugehörigen pro-Kopf-Größen konstant halten will.
Literaturverzeichnis
- Anderson (1993)
- Anderson, G. S.: Symbolic Algebra Programming for Analyzing the
Long Run Dynamics of Economic Models.
In: Varian, H. R. (Hrsg.): Economic and
Financial Modeling with Mathematica, S. 124-147 (Chapter 6). New York :
Springer, 1993.
- Barro, Sala-i-Martin (1998)
- Barro, R. J. ; Sala-i-Martin, X.:
Wirtschaftswachstum.
München : Oldenbourg, 1998.
- Böckmann, Rettig (1998)
- Böckmann, L. ; Rettig, R.: Makroökonomisches
Gesamtmodell.
In: das wirtschaftsstudium (Studienblatt), (1998).
- Dernburg, McDougall (1981)
- Dernburg, T. F. ; McDougall, D. M.: Lehrbuch
der Makroökonomischen Theorie.
3. Aufl.
Stuttgart : Fischer, 1981.
- Dieckheuer (1998)
- Dieckheuer, G.: Internationale Wirtschaftsbeziehungen.
4. Aufl.
München : Oldenbourg, 1998.
- Felderer, Homburg (1999)
- Felderer, B. ; Homburg, S.: Makroökonomik und
neue Makroökonomik.
7. Aufl.
Berlin : Springer, 1999.
- Jarchow (1993)
- Jarchow, H.-J.: Theorie und Politik des Geldes. Bd. 1 :
Geldtheorie.
9. Aufl.
Göttingen : Vandenhoeck & Ruprecht, 1993.
- Lehnert (1999)
- Lehnert, B.: KDE- und Qt-Programmierung: GUI-Entwicklung
für Linux.
München : Addison-Wesley, 1999.
- Mankiw (1998)
- Mankiw, N. G.: Makroökonomik.
3. Aufl.
Stuttgart : Schäfer-Pöschel, 1998.
- Mercado, Kendrick, Amman (1998)
- Mercado, P. R. ; Kendrick, D. A. ; Amman,
H.: Teaching Macroeconomics with GAMS.
In: Computational Economics, 12 (1998), S. 125-149.
- Otruba, Munduch, Stiassny (1996)
- Otruba, H. ; Munduch, G. ; Stiassny, A.:
Makroökonomik.
2. Aufl.
Wien : Springer, 1996.
- Ott, Ott, Yoo (1983)
- Ott, D. J. ; Ott, A. F. ; Yoo, J. H.:
Macroeconomic Theory.
University Press of America : Lanham, 1983.
- Sachs, Larrain (1993)
- Sachs, J. D. ; Larrain, F.: Macroeconomics in
the Global Economy.
New York : Harvester, 1993.
- Sargent (1994)
- Sargent, T. J.: Makroökonomik.
München : Oldenbourg, 1994.
- Schumann, Meyer, Ströbele (1999)
- Schumann, J. ; Meyer, U. ; Ströbele, W.:
Grundzüge der mikroökonomischen Theorie.
7. Aufl.
Berlin : Springer, 1999.
- Siebert (1994)
- Siebert, H.: Außenwirtschaft.
6. Aufl.
Stuttgart : Fischer, 1994.
- Stobbe (1994)
- Stobbe, A.: Volkswirtschaftliches Rechnungswesen.
8. Aufl.
Berlin : Springer, 1994.
- Woll (2000)
- Woll, A.: Allgemeine Volkswirtschaftslehre.
13. Aufl.
München : Vahlen, 2000.

|
 See more details |
| Gesamtübersicht. |
Fußnoten:
1Das Finanzierungskonto resultiert aus der Konsolidierung des Vermögensänderungskontos und des Kreditänderungskontos. Dabei gehen auf gesamtwirtschaftlicher Ebene die Informationen über Finanzierungssalden und Kreditverflechungen verloren. Vgl. Stobbe (1994,S. 97 ff.).
2Die in den Text eingebetteten Abbildungen und Icons sind Ausschnitte der Programmoberfläche, die in der Abbildung 9 dargestellt wird. Aus technischen Gründen weichen die mathematischen Symbole des Programms von der üblichen Schreibweise ab. Diese Differenzen werden im Text beispielsweise durch Caut ≡ C0 hervorgehoben.
3In Anlehnung an Fisher ergibt sich der reale Zinssatz i, indem man die (erwartete) Inflationsrate π = (Pt+1−Pt)/Pt vom nominalen Zinssatz r abzieht, i = r−π. Die Beziehung stellt sich als Approximation für den realen Zinssatz i heraus, sofern die Definitionsgleichung 1+i = (1+r)Pt/Pt+1 wie in Sachs, Larrain (1993,S. 227) unterstellt wird. Durch einfache Umrechnung folgt r = π+(1+π)i, wobei iπ ≈ 0 angenommen wird. Solange man von konstanten Preisen ausgeht (π = 0), ist eine Unterscheidung zwischen dem realen und dem nominalen Zinssatz unnötig.
4Auch die Vorsichtskasse wird hauptsächlich vom Volkseinkommen Y bestimmt und daher unter das Transaktionsmotiv subsumiert, vgl. hierzu Jarchow (1993,S. 90-97). Eine ähnliche graphische Darstellung, die die Vorsichtskasse explizit berücksichtigt findet man in Otruba, Munduch, Stiassny (1996,S. 175).
5Im sogenannten Baumol-Tobin-Modell wird auf schlüssige Weise dargelegt, dass die Nachfrage nach Transaktionskasse auch vom Zinssatz abhängt. Vgl. hierzu etwa Mankiw (1998,S. 539-541).
6Die Idee der diversifizierten Geldnachfrage geht auf Tobin und Markowitz zurück und kann in Ott, Ott, Yoo (1983, S. 185-192) nachgelesen werden. Dort werden Kriterien abgeleitet wie die optimale Zusammensetzung eines Portfolios aussieht, wenn die beiden enthaltenen Aktiva - Geld und Wertpapiere - durch unterschiedliche Risiken und Erträge gekennzeichnet sind.
7Die effektive Verzinsung ρ eines Wertpapiers mit dem
Nennwert Z und dem nominalen Zinssatz r ist gegeben durch
|
wobei k den Kurs des Wertpapiers bezeichnet.
Dagegen muss die reale Verzinsung auch Änderungen des Preisniveaus,
also die Inflationsrate π = (Pt+1−Pt)/Pt, berücksichtigen:
|
Insbesondere bei konstanten Preisen (π = 0) erhält man, i = ρ. Gleichzeitig ist der reale Zinssatz i um so höher, je kleiner der Kurswert kt ist. Ähnlich zur Fisher-Gleichung in der Fußnote 3 erhält man für π ≠ 0 approximativ i = ρ−π, wobei iπ ≈ 0 unterstellt wird.
8Der Schieberegler für das Preisniveau ist der Abbildung 9 zu entnehmen.
9Wird die nominale Ersparnis PtS mit dem nominalen Zinssatz r verzinst, dann kann der Haushalt eine Periode später den Betrag (1+r)PtS/Pt+1 zu konsumptiven Zwecken verwenden. Unter Berücksichtigung der Approximiation aus der Fußnote 3 lautet der Konsum der Periode t+1, in der nicht gearbeitet wird, Ct+1 = (1+i)St. Im optimalen intertemporalen Verbrauchsplan, wie ihn Schumann, Meyer, Ströbele (1999,S. 111 ff.) behandeln, hängt der heutige Konsum neben dem heutigen Einkommen insbesondere auch vom realen Zinssatz i ab. Diese Sicht wird von der klassischen Theorie betont.
10In der Realität ist das Preisniveau P keine Instrumentvariable, die sich exogen einstellen lässt. Allerdings werden viele Effekte erst sichtbar, wenn man P zumindest kurzfristig konstant hält.
11In
Sargent (1994) wird gezeigt, wie der nominale Aktienwert V zum
Zeitpunkt t berechnet wird. In Anlehnung an das Tobinsche q erhält man
unter Vernachlässigung von Abschreibungen
|
Wenn also der reale Zinssatz mit der Grenzleistungsfähigkeit des Kapitals übereinstimmt, dann entspricht der nominale Aktienwert V dem nominalen Wert des Kapitalstocks PKK, d.h. q = 1.
12Aktien und staatliche Schuldverschreibungen werden als perfekte Substitute angesehen.
13Felderer, Homburg (1999) sprechen vom Kapitalmarkt, wobei sie die Ersparnis mit dem Kapitalangebot gleichsetzen und die Investition als Kapitalnachfrage bezeichnen.
14Wie Jarchow (1993,S. 326) betont, ist das Saysche Theorem ein Spezialfall des Walras-Gesetzes.
15Die Funktion für den internationalen Kapitalverkehr ist Dieckheuer (1998,S. 175) entnommen worden, sie vernachlässigt Entscheidungen über optimale Portfoliostrukturen.


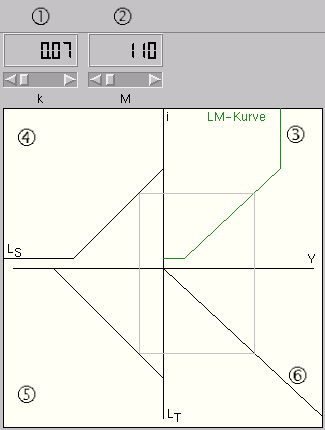 Abbildung 3: Geldmarkt
Abbildung 3: Geldmarkt