Grenzrate der Substitution im Konsum (GRS)
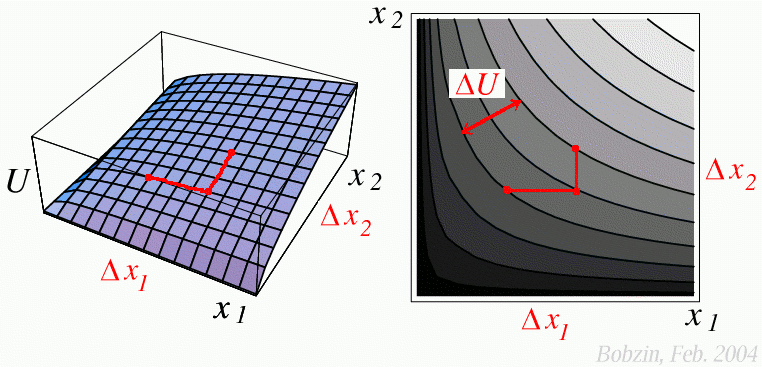
(1) Ökonomisch gibt die Grenzrate der Substitution im Konsum (GRS) zwischen zwei Gütermengen an, um wie viele Einheiten $\Delta x_2$ die Gütermenge x2 erhöht (gesenkt) werden muss, wenn bei konstantem Nutzenniveau U die Gütermenge x1 um eine (infinitesimal kleine) Einheit $\Delta x_1$ reduziert (erhöht) wird.
(2) Geometrisch kann man sich diese Gütersubstitution als einen Schritt
von P nach Q entlang der Indifferenzkurve, die zu U gehört, vorstellen.
(3) Mathematisch entspricht die GRS der Steigung einer
Indifferenzkurve im Punkt
P = (x1,x2).
Bilde das totales Differential der Nutzenfunktion $U = u(x_1,x_2)$. \[ \d U =\ \abl{u(x_1,x_2)}{x_1}\ \d x_1\ +\ \abl{u(x_1,x_2)}{x_2}\ \d x_2 \]
Auf einer Indifferenzkurve ist U = konstant, also dU = 0. Damit folgt
durch bloße Umstellung
\[
\text{GRS} = -\ \frac{\d x_2}{\d x_1}
\ =\ \frac{\abl{u(x_1,x_2)}{x_1}}{\abl{u(x_1,x_2)}{x_2}}
\]
so wie es der Satz der impliziten
Differentiation besagt.
Grafische Darstellung:
Bilde das totales Differential der Nutzenfunktion $U = u(x_1,x_2)$. \[ \d U =\ \abl{u(x_1,x_2)}{x_1}\ \d x_1\ +\ \abl{u(x_1,x_2)}{x_2}\ \d x_2 \]
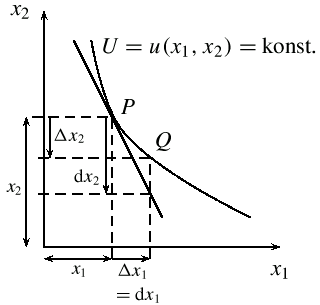
Nutzenmaximierung
Ausgabenminimierung
GRiS: Grenzrate der intertemporalen Substitution
GRS: Grenzrate der technischen Substitution