Unternehmen
Unternehmen stellen Güter mit Hilfe bestimmter Produktionsfaktoren her.
Vereinfachend wird häufig angenommen, dass jedes Unternehmen ein einziges Gut
produziert. Der Transformationsprozess zwischen den Inputs $(v_1,v_2,...,v_m)$
und dem Output $x$ wird durch die
Produktionsfunktion beschrieben, wobei die Produktionsfunktion nur technisch
effiziente Aktivitäten $(x,v_1,v_2,...,v_m)$ angibt.
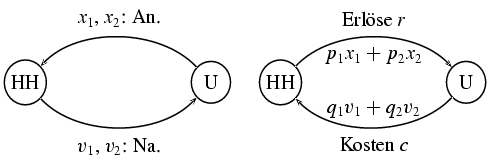
Durch den Verkauf des Gutes (an
Haushalte oder andere Unternehmen) erzielen
die Unternehmen Erlöse $r=px$, wobei $p$ den Preis des Gutes $x$ bezeichnet.
Diesem Erlös stehen die Faktorkosten $c=q_1v_1+q_2v_2+...+q_mv_m$ gegenüber,
worin $q_i$ $(i=1,...,m)$ den Preis einer Einheit der Produktionsfaktors $v_i$
angibt. Die Differenz zwischen Erlösen und Kosten nennt man den Gewinn
\[
\pi=r-c=px-q_1v_1-q_2v_2-...-q_mv_m
\]
Zunächst wird unterstellt, dass jedes Unternehmen das Ziel der
Gewinnmaximierung verfolgt. Sind der Güterpreis
$p$ sowie die Faktorpreise $q_i$ gegeben, dann steht das Unternehmen vor dem
Problem, eine geeignete Aktivität $(x,v_1,v_2,...,v_m)$ bestehend aus der
Gütermenge und den Faktormengen zu wählen. In jedem Fall muss eine
zulässige Aktivität gewählt werden,
was immer dann gewährleistet ist, wenn die
Produktionsfunktion
$x=x(v_1,v_2,...,v_m)$ liefert. Unter allen zulässigen Aktivitäten ist nun
irgendeine Aktivität auszuwählen, die den Gewinn $\pi$ maximiert. Man sagt,
dass sich das Unternehmen als
Mengenanpasser
verhält, weil es die Gütermenge und die Faktormengen mit den gegebenen Preisen
$(p,q_1,q_2,...,q_m)$ in Einklang bringen muss.
Die Gütermengen aller gewinnmaximalen Aktivitäten einer Unternehmung
determinieren das
Güterangebot. Dieses
Angebot variiert mit dem Güterpreis und es hängt von den Faktorpreisen ab.
Jede Ausbringungsmenge kann in der Regel durch verschiedene
Faktorkombinationen (
Isoquante) realisiert
werden. Man beachte, dass sich ein Gewinnmaximum nur dann realisieren lässt,
wenn der Output zu minimalen Kosten (
Kostenfunktion) hergestellt wird. Die entsprechende
Minimalkostenkombination der Faktoren determiniert
die
Faktornachfrage in Abhängigkeit von
den Faktorpreisen und der herzustellenden Gütermenge.
Angebotsmonopol (Preisabsatzfunktion $p=p(x)$)
Nachfragemonopol (Preisbeschaffungsfunktion $q_i=q_i(v_i)$)