Isoquante
Ausgangspunkt ist die
Produktionsfunktion einer Einproduktunternehmung
\[
x=x(v_1, v_2)
\]
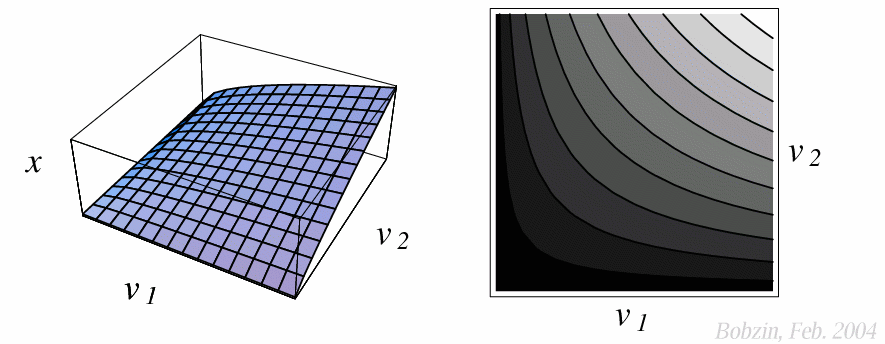
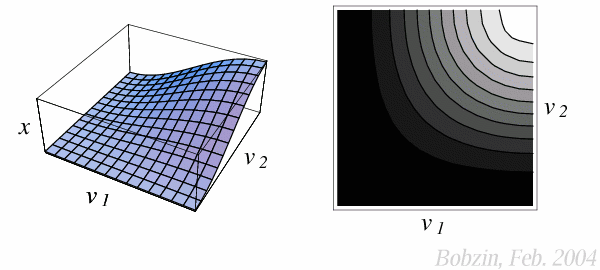
Typische Gestalten von Produktionsgebirgen sind den folgenden Grafiken zu
entnehmen.
Ertragsgesetz
Die
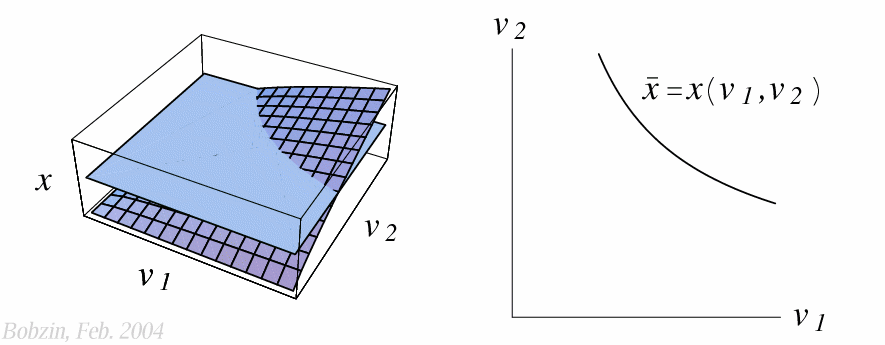
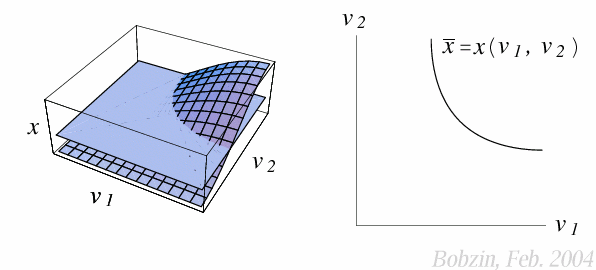
Isoquante ist der geometrische Ort aller
Faktorkombination $(v_1, v_2)$, bei denen der Output $\bar x$ konstant ist.
\[
\bar x=x(v_1, v_2) \implies
v_2=x^{-1}(v_1, \bar x) \implies v_2=g(v_1)
\]
Die
Steigung $g'(v_1)$ einer Isoquante
(
GRS) lässt sich über den
Satz der impliziten Differentiation
bestimmen.
GRS: Grenzrate der technischen Substitution
implizite Differentiation
Indifferenzkurve (Theorie des Haushalts)