Angebotsmonopol
Das
Angebotsmonopol ist eine
Marktform, bei der viele Nachfrager einem einzigen Anbieter gegenüberstehen,
wobei der Monopolist weiß, wie seine
Preis-Absatz-Funktion
$p = p(x)$ (also die inverse Funktion der Marktnachfrage) lautet. Außer seinen
Produktionskosten $c(x)$ kennt der Monopolist damit seinen Umsatz in
Abhängigkeit von der Menge: $r(x) = p(x) x$. Verfolgt der Monopolist das Ziel
der Gewinnmaximierung, dann muss er folgendes Problem lösen:
\[
\max\ p(x) x - c(x)
\]
Eine notwendige Bedingung verlangt, die erste Ableitung gleich 0 zu setzen. Man
erhält
\[
r'(x^*) = p'(x^*) x^* + p(x^*) = c'(x^*)
\]
Ist auch die hinreichende Bedingung, dass nämlich die zweite Ableitung an der
Stelle $x^*$ kleiner als 0 ist, erfüllt, dann liefert der
Cournotsche Punkt $(x^*,p(x^*))$ ein Gewinnmaximum.
In der Regel wird die notwendige Bedingung über die
Amoroso-Robinson-Relation ausgedrückt. Hierzu
wird der Grenzerlös auf der rechten wie folgt umgeformt
\[
r'(x^*) =\ \left(\frac{\d p(x^*)}{\d x}\ \frac{x^*}{p(x^*)}+1\right) p(x^*)
=\ \left(\frac{1}{\eta_{xp}}+1\right) p(x^*),
\]
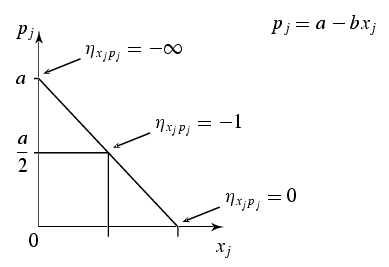
wobei $\eta_{xp}$ die
direkte Preiselastizität
der Nachfrage bezeichnet.
Bei einer linear fallenden Preis-Absatz-Funktion mit $p = a-bx$ lautet der
Erlös $r(x) = ax - bx^2$. Damit hat der Grenzerlös $r'(x) = a-2bx$ die
doppelte Steigung der Preis-Absatz-Funktion, so wie es die folgende Abbildung
darstellt.
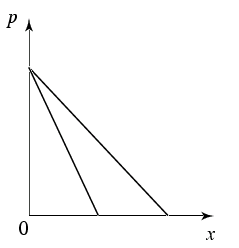
Der
Cournotsche Punkt lässt sich nun geometrisch ermitteln,
indem man die Kurve der Grenzkosten hinzufügt und den Schnittpunkt
$r'(x^*) = c'(x^*)$ bestimmt. Senkrecht über dem Schnittpunkt auf der
Preis-Absatz-Funktion findet man den mit $C$ bezeichneten Cournotschen Punkt
$(x^*,p(x^*))$.
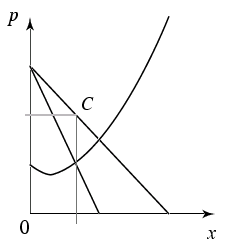
Wie die Grafik zeigt, liegt der Cournotsche Punkt immer im elastischen Bereich
der Preis-Absatz-Funktion, d.h. $\eta_{xp}<-1$. Formal ergibt sich dieser
Tatbestand aus der Beobachtung, dass die Grenzkosten $c'$ immer positiv sind,
so dass
\[
\left(\frac{1}{\eta_{xp}}+1\right)\ p(x^*) = c'(x^*) > 0.
\]
Da auch $p(x^*)>0$ gilt, muss der Klammerausdruck auf der linken Seite positiv
sein. Durch einfache Umformung erhält man $\eta_{xp}<-1$.
Für einen Vergleich mit dem Marktergebnis bei vollständiger Konkurrenz
unterstellt man nun, dass der steigende Ast der Grenzkostenkurve des
Monopolisten mit der aggregierten Angebotskurve (= Summe aller
Grenzkostenkurven der einzelnen Anbieter) bei vollständiger Konkurrenz
übereinstimmt. Da sich die Anbieter nun als Mengenanpasser verhalten, lautet
die notwendige Bedingung für ein Gewinnmaximum nun $p = p(x^*) = c'(x^*)$.
Dieses Ergebnis der
Als-Ob-Konkurrenz
besagt, dass ein Monopolist weniger als die Anbieter bei vollständiger
Konkurrenz anbietet. Außerdem wird für das geringere Angebot ein höherer Preis
verlangt. (Vergleiche in der zweiten Abbildung den Cournotschen Punkt mit dem
Schnittpunkt der Preis-Absatz-Funktion und der Grenzkostenkurve.)
Monopolistische Ausbeutung:
Bemerkenswerterweise bittet der Monopolist nicht nur die Konsumenten zur
Kasse, auch die eingesetzten Produktionsfaktoren (hier $v_1$ und $v_2$) werden
monopolistisch ausgebeutet. Hierzu wird das Problem der Gewinnmaximierung von
der Faktoreinsatzseite analysiert:
\[
\max_{v_1,v_2} p(x(v_1,v_2)) x(v_1,v_2) - q_1v_1 - q_2v_2
\]
Konzentriert man sich auf den ersten Produktionsfaktor, dann lautet eine
notwendige Bedingung für ein Gewinnmaximum
\[
\frac{\d p(x)}{\d x}\ \abl{x(v_1^*,v_2^*)}{v_1}\ x(v_1^*,v_2^*)
+ p(x)\ \abl{x(v_1^*,v_2^*)}{v_1}\ - q_1 = 0.
\]
Durch einfache Umstellung folgt
\[
q_1 =\ \left(\frac{\d p(x)}{\d x}\ \frac{x(v_1^*,v_2^*)}{p(x)}+1\right)\
p(x)\ \abl{x(v_1^*,v_2^*)}{v_1}\ =\ \left(\frac{1}{\eta_{xp}}+1\right)\
p(x)\ \abl{x(v_1^*,v_2^*)}{v_1}.
\]
Während die Produktionsfaktoren bei vollständiger Konkurrenz entsprechend
ihrer
monetären Grenzproduktivität entlohnt
werden (
siehe hier), müssen sie nun entweder bei
gleichen Faktorpreisen mehr leisten oder sie erhalten bei gleicher Leistung
eine niedrigere Entlohnung. D.h. wegen $\eta_{xp}<-1$
\[
q_1 =\ \left(\frac{1}{\eta_{xp}}+1\right)\ p(x)\ \abl{x(v_1^*,v_2^*)}{v_1}\ <\
p(x)\ \abl{x(v_1^*,v_2^*)}{v_1}.
\]
natürliches Monopol
Als-Ob-Konkurrenz




