Präferenzen
Im Alltag muss jeder Haushalt ständig zwischen den verschiedensten
Warenkörben oder Güterbündeln abwägen. Dabei bestehen sämtliche Güterbündel
aus $n$ Gütermengen $x_j$ mit $j = 1\BIS n$, die sich als Vektoren
darstellen lassen.
\[
\vx\ = (x_1\BIS x_n)\T
\]
Man beachte, dass nicht jedes Güterbündel das Gut $j$ enthalten muss, die
entsprechende Menge $x_j$ ist dann gleich null.
Wie der Vergleich zwischen den Güterbündel ausfällt, hängt von den Vorlieben
oder Präferenzen des Haushalts ab.
- Das Güterbündel $\vx'$ wird dem Güterbündel $\vx''$
vorgezogen oder präferiert, d.h., $\vx'$ ist besser als
$\vx''$.
\[
\vx'>_P \vx''
\]
- Der Haushalt ist indifferent
zwischen beiden Güterbündeln, d.h., $\vx'$ ist genauso gut wie $\vx''$.
\[
\vx'\ \sim_P\ \vx''
\]
- Das Güterbündel $\vx'$ ist genauso gut wie oder besser als das
Güterbündel $\vx''$. D.h. umgekehrt, $\vx''$ ist nicht schlechter als $\vx'$.
\[
\vx'\geq_P \vx''
\]
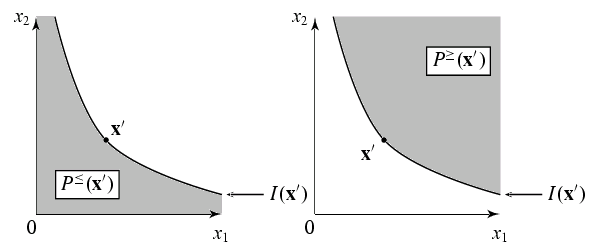
Ausgehend von einem beliebigen Güterbündel $\vx'$ lassen sich die beiden
sogenannten Konturmengen definieren:
\[
P^\geq(\vx') =\ \{\vx|\ \vx\geq_P \vx'\} \quad\text{und}\quad
P^\leq(\vx') =\ \{\vx|\ \vx\leq_P \vx'\}
\]
Darüber hinaus ist die
Indifferenzkurve wesentlicher
Bestandteil der Analyse,
\[
I(\vx') =\ \{\vx|\ \vx\ \sim_P\ \vx'\}.
\]
In der Regel wird unterstellt, dass die Präferenzen den folgenden sechs
Axiomen genügen:
Vollständigkeit:
Für zwei beliebige Güterbündel $\vx'$, $\vx''$
gilt entweder $\vx'\geq_P \vx''$, $\vx''\geq_P \vx'$ oder beides, d.h.
$\vx'\ \sim_P\ \vx''$.
Reflexivität:
Zwei identische Güterbündel können nicht unterschiedlich
bewertet werden, $\vx\geq_P \vx$.
Transitivität:
Für drei Güterbündel $\vx'$, $\vx''$ und $\vx'''$ gilt
\[
\left[\vx'\geq_P \vx''\quad\text{und}\quad \vx''\geq_P \vx'''\right] \implies
\vx'\geq_P \vx'''
\]
Stetigkeit:
Von den Konturmengen $P^\geq(\vx')$ und $ P^\leq(\vx')$
wird angenommen, dass sie abgeschlossen sind (d.h., der Rand oder genauer die
Indifferenzkurve gehört zu der jeweils betrachteten Menge.)
Insbesondere die obere Konturmenge $P^\geq(\vx')$ enthält alle Güterbündel,
die besser als $\vx'$ sind, und außerdem die Indifferenzkurve $I(\vx')$.
Nichtsättigung:
Zu jedem Güterbündel $\vx'$ existiert ein präferiertes
Güterbündel $\vx''$, d.h. $\vx''>_P \vx'$.
Konvexität:
Für zwei beliebige Güterbündel $\vx'$, $\vx''$ mit
$\vx'\geq_P \vx''$ gilt
\[
\lambda \vx'+(1-\lambda)\vx''\geq_P \vx''\quad\text{für alle}\ \ 0\leq\lambda\leq 1
\]
Damit ist jede obere Konturmenge $P^\geq(\vx)$ konvex. Man beachte, dass
die Annahme der Konvexität voraussetzt, dass sich sämtliche Gütermengen in
beliebig kleine Bestandteile zerlegen lassen.
In der Regel wird das Axiom der Nichtsättigung durch die etwas schärfere
Version der Monotonie ersetzt: Wenn mehr besser ist, dann
kann ein Güterbündel $\vx'$, das mindestens so groß ist wie $\vx''$, nicht
schlechter als $\vx''$ sein.
\[
\vx'\geq\vx''\implies \vx'\geq_P \vx''
\]
Wichtig: Wenn man die ersten vier Axiome akzeptiert, dann ist
die Existenz einer stetigen Nutzenfunktion
garantiert. Das heißt, die Präferenzen lassen sich durch eine Nutzenfunktion
$u(\vx)$ mit der Eigenschaft
\[
\vx'\geq_P \vx'' \iff u(\vx')\geq u(\vx')
\]
repräsentieren. Den Beweis hat Debreu 1954 vorgestellt.
Die Konvexität stellt darüber hinaus sicher, dass die Nutzenfunktion
quasi-konkav ist. Damit hat die Nutzenfunktion konvexe Niveaulinien
bzw. konvexe Indifferenzkurven. Ökonomisch ausgedrückt, entsprechen konvexe
Indifferenzkurven einer abnehmenden Grenzrate der
Substitution (GRS).
Geschichte der Nutzentheorie (englisch)