Metrische Nutzenfunktion
Ausgangspunkt ist die
indirekte
Nutzenfunktion, die das maximal erreichbare
Nutzenniveau $U'$ angibt, wenn die Preise $\vp'$ herrschen und das Einkommen
$y'$ gegeben ist.
\[
U' = v(\vp', y')
\]
Ökonomen stehen nun vor dem Problem, wie sich der Nutzen verändert, wenn die
Preise ($\vp' \to \vp''$) oder das Einkommen ($y' \to y''$) variieren, wobei
die Nutzendifferenz
\[
\Delta U = v(\vp'', y'') - v(\vp', y')
\]
für ordinale Nutzenfunktionen inhaltsleer ist. Dieses Problem lässt sich
umgehen, indem man mit Hilfe der
Ausgabenfunktion $e(\vp'', U')$ die
indirekte metrische Nutzenfunktion (indirect money metric
utility function)
\[
\mu(\vp''; \vp', y') = e(\vp'', v(\vp', y'))
\]
definiert. Diese Funktion wird
in Geldeinheiten gemessen und
sie gibt an, wie hoch das neue Einkommen bei den neuen Preisen $\vp''$ sein
muss, damit sich der Haushalt genauso wohl fühlt, wie in der Ausgangssitution
mit den Preisen $\vp'$ und dem Einkommen $y'$. Damit muss gleichzeitig
\[
\mu(\vp; \vp, y) =y
\]
erfüllt sein.
Nun kann man eine Größe angeben, die die Nutzendifferenz in Geldeinheiten
ausdrückt.
\[
\mu(\vp; \vp'', y'') - \mu(\vp; \vp', y')
\]
Man beachte, dass sich der erste Ausdruck auf das
konstante
Nutzenniveau $U''=v(\vp'', y'')$ bezieht, so wie der zweite Ausdruch auf dem
konstanten Nutzenniveau $U'=v(\vp', y')$ beruht.
Damit ergeben sich zwei Maße für die Nutzendifferenz.
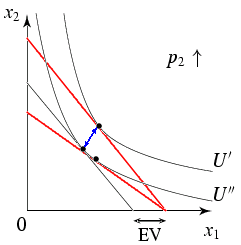
- Die äquivalente Variation (Equivalent
Variation) konzentriert sich auf die ursprünglichen
Preise $\vp'$ und das ursprüngliche Einkommen $y'$.
\[
EV = \mu(\vp'; \vp'', U'') - \mu(\vp'; \vp', U') = \mu(\vp'; \vp'', U'') - y'
\]
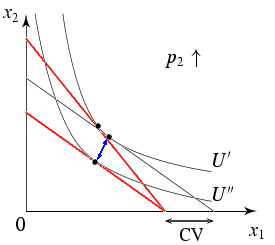
- Dagegen macht die kompensierende Variation
(Compensating Variation) eine Aussage über
die neuen Preise $\vp''$ und das neue Einkommen $y''$
\[
CV = \mu(\vp''; \vp'', U'') - \mu(\vp''; \vp', U') = y'' - \mu(\vp''; \vp', U')
\]
Beide Maße liefern in der Regel unterschiedliche Approximationen für den
"Abstand zwischen den Indifferenzkurven", da sie von unterschiedlichen
Punkten ausgehen.
Konsumentenrente