Indifferenzkurve
Eine
Indifferenzkurve beschreibt den geometrische Ort aller
Güterkombinationen, die der Haushalt gemäß seinen
Präferenzen als
gleichwertig einschätzt.
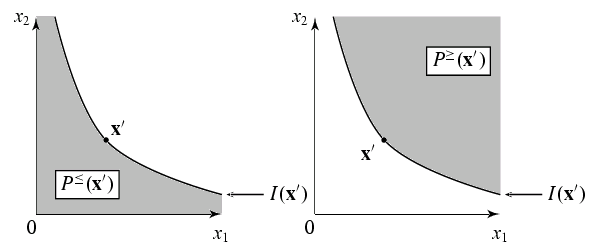
Ausgehend von einem Güterbündel $\vx'$ lautet die Indifferenzkurve
\[
I(\vx') = \{\vx|\ \vx\sim_P \vx'\}.
\]
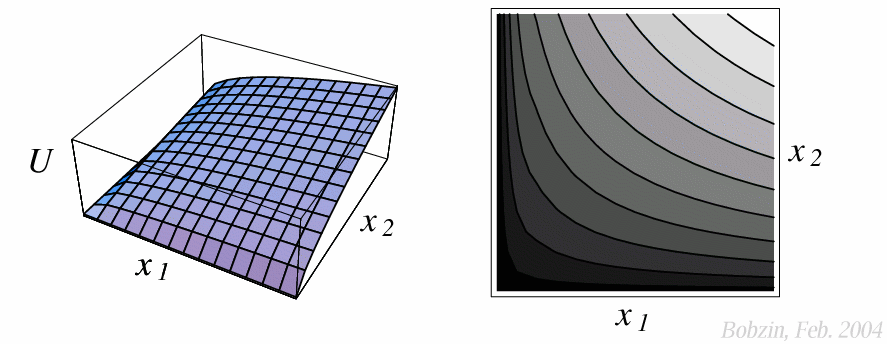
Übertragen auf die entsprechende
Nutzenfunktion $u$ ergibt sich
\[
\vx\in I(\vx') \iff u(\vx) = u(\vx') = U = \text{konst.}
\]
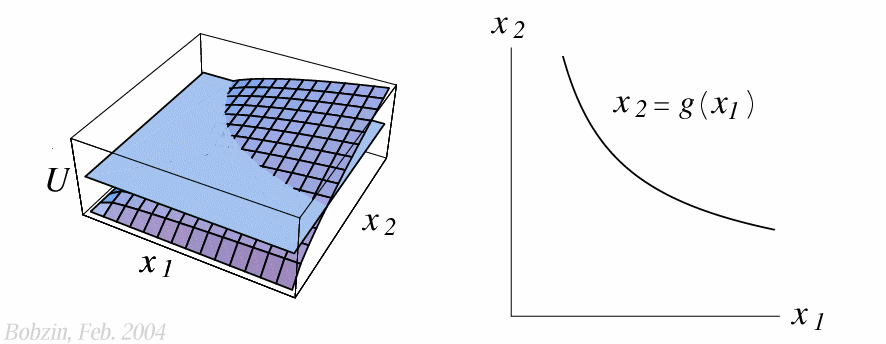
Die Indifferenzkurve für das konstante Nutzenniveau $U^K$ kann nun explizit
angegeben werden.
\[
U^K = u(x_1,x_2) \implies x_2 = u^{-1}(x_1,U^K) \implies x_2 = g(x_1)
\]
Die
Steigung $g'(x_1)$ einer Indifferenzkurve
(
GRS) lässt sich über den
Satz der impliziten Differentiation
bestimmen.