Satz der impliziten Differentiation
Totales Differential einer impliziten Funktion
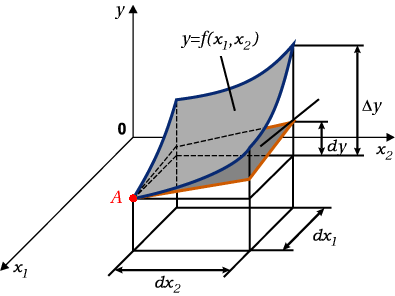
$f(x_1,x_2,y) = 0$
\[
0 =\ \abl{f(x_1,x_2,y)}{x_1}\ \d x_1 + \abl{f(x_1,x_2,y)}{x_2}\ \d x_2 +\
\abl{f(x_1,x_2,y)}{y}\ \d y
\]
Falls $y$ konstant ist $(\d y = 0)$, dann folgt
\[
\frac{\d x_2}{\d x_1}\ = -\ \frac{\abl{f(x_1,x_2,y)}{x_1}}{\abl{f(x_1,x_2,y)}{x_2}}
\]
Da $y$ unverändert bleibt, bewegt man sich auf der entsprechenden Niveaulinie.
Die Steigung dieser Niveaulinie $\d x_1/\d x_2$ lässt sich über die implizite
Differentiation ermitteln. Bitte beachten Sie das
Minuszeichen!
Beispiele:
- Die Grenzrate der Substitution (GRS) zwischen zwei Konsumgütern
entspricht der Steigung einer Indifferenzkurve.
Berechnung der GRS
- Die Grenzrate der intertemporalen Subsitution (GRiS) bezeichnet die
Steigung einer Indifferenzkurve zur intertemporalen
Nutzenfunktion $U = u(e_t,e_{t+1})$.
Berechnung der GRiS
- Die Grenzrate der technischen Subsitution (GRS) zwischen zwei
Produktionsfaktoren entspricht der Steigung einer
Isoquante.
Berechnung der GRS