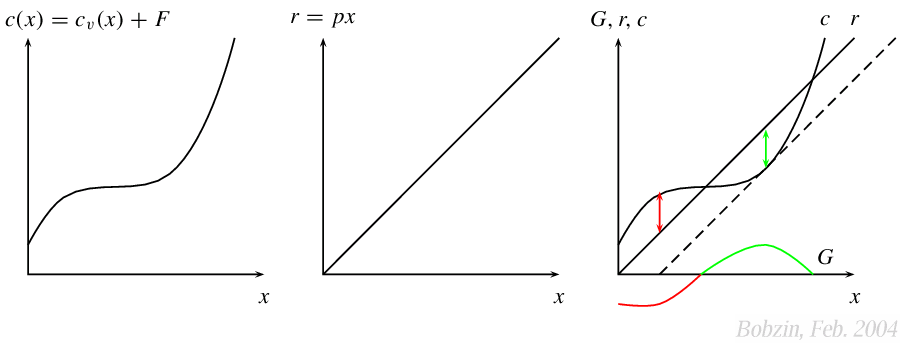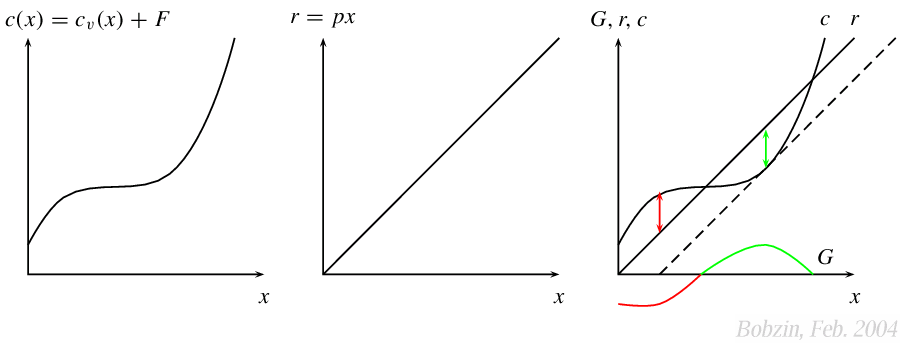Gewinnmaximierung von der Outputseite
1. Totale Faktorvariation
Die Zielfunktion $G$ enthält die Produktionsfunktion $x(v_1, v_2)$ auf der Kostenseite. Nachdem die
Kostenfunktion
\[
c(q_1, q_2, x) = \min \left\{q_1v_1 + q_2v_2\ |\ x=x(v_1, v_2)\right\}
\]
berechnet worden ist, lautet das Problem der Gewinnmaximierung
\[
G(x)=p x - c(q_1, q_2, x) \to \text{Max}
\]
Die Lösung dieses Maximierungsproblems ist die Gewinnfunktion
\[
\pi(p, q_1, q_2) = \max_{x} G(x),
\]
sie hängt von den konstanten Preisen $p$, $q_1$ und $q_2$ (also den Parametern
des Problems) ab.
Beachte: Wenn auf diesem Weg der Gewinn maximiert wird, dann
muss zuvor das Problem der Kostenminimierung gelöst worden sein.
Im Gewinnmaximum stimmt der Güterpreis mit den Grenzkosten überein:
\[
p = \abl{c(q_1, q_2, x)}{x}
\]
Die hinreichende Bedingung zweiter Ordnung für ein Gewinnmaximum
\[
\abl{^2G(x)}{x^2} = -\abl{^2c(q_1, q_2, x)}{x^2}<0
\]
verlangt, das man sich auf dem steigenden Ast der Grenzkostenkurve befindet!
2. Partielle Faktorvariation
Wenn $v_2$ einen fixen Faktor bezeichnet (mit Fixkosten $F=q_2v_2$), dann
lautet das Problem der Gewinnmaximierung
\[
G(x)=p x - c_v(x)-F \to \text{Max}
\]
Grafische Lösung für einen ertragsgesetzlichen Verlauf der Kostenfunktion
$c(x)=c_v(x)+F$.
Kostenfunktion (ertragsgesetzlicher Verlauf)
Kostenfunktion
Grenzkosten
Erlösfunktion
Gewinnmaximierung von der Inputseite