Autarkiegleichgewicht

1 Allgemeine Beschreibung

Ein Autarkiegleichgewicht bezeichnet ein allgemeines Konkurrenzgleichgewicht für eine geschlossene Volkswirtschaft (also kein Außenhandel), in dem alle Güter- und Faktormärkte simultan ausgeglichen sind. Hierzu müssen auf sämtlichen Märkten Gleichgewichtspreise vorliegen. Demnach sind alle Produktionsfaktoren vollbeschäftigt und alles, was der Produktionssektor herstellt wird von den Haushalten nachgefragt.

Autarkiegleichgewichte dienen als Referenzlösung für den Vergleich mit allgemeinen Konkurrenzgleichgewichten bei Freihandel. Da man insbesondere die Effekte eines internationalen Gütertauschs bestimmen möchte, werden in einem ersten Schritt alle analytischen Probleme beseite geschoben, die vor allem die Marktform im Produktionssektor, die Einkommensverteilung im Haushaltssektor und die nationalen Faktormärkte betreffen, und die einer gesonderten Analyse bedürfen.

vollständige Konkurrenz im Produktionssektor
identische homothetischen Nutzenfunktionen aller Haushalte
vollkommen preisunelastisches Faktorangebot

2 Der Fall zweier Güter und zweier Faktoren

Eine vereinfachte Darstellung geht von zwei Gütern $x_1$ und $x_2$ sowie zwei Produktionsfaktoren $v_1$ und $v_1$ aus.

(1) Produktion

Die Güter werden in zwei Sektoren hergestellt, die jeweils ein Gut produzieren und die sektorspezifische linear-homogene Produktionsfunktion $f_j\ \ (j=1,2)$ haben. \[ x_j=f_j(v_{1j},v_{2j})\qquad (j=1,2) \] (Steigende Skalenerträge (überlinear-homogene Produktionsfunktionen) werden hier ausgeschlossen, weil sie mit der Marktform der vollständigen Konkurrenz nicht zu vereinbaren sind.)

Bei Vollbeschäftigung der Faktoren müssen die gesamtwirtschaftlich angebotenen Mengen $v_1$ und $v_2$ mit den gesamten Verbräuchen übereinstimmen. \[ v_1=v_{11}+v_{12}\quad\text{und}\quad v_2=v_{21}+v_{22} \] Noch bevor irgendein Optimierungsproblem gelöst wird, lassen sich zwei hifreiche graphische Zwischenergebnisse anführen.

Fakorallokation: Die Edgeworth-Box zeigt an, wie die Faktorbestände auf die beiden Sektoren verteilt werden. Siehe Graphik.
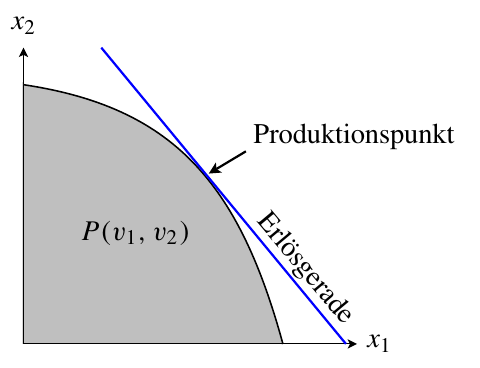
Menge möglicher Produktionspunkte: Alle mit den gegebenen Faktorbeständen und den gegebenen Produktionsfunktionen herstellbaren Güterkombinationen lassen sich im Güterraum kennzeichnen. Siehe Graphik.

Das Güterangebot order auch Produktionspunkt \[ x_1^A=x_1^A(p_1,p_2,v_1,v_2)\quad\text{und}\quad x_2^A=x_2^A(p_1,p_2,v_1,v_2) \] und damit auch die sektorale Faktornachfrage ergeben sich aus dem Kalkül der gesamtwirtschaftlichen Erlösmaximierung, wobei die Güterpreise $p_1$ und $p_2$ sowie die nationalen Faktorbestände $v_1$ und $v_2$ gegeben sind.

Beachte: Die individuelle Gewinnmaximierung wird hier durch das einfachere Problem der gesamtwirtschaftlichen Erlösmaximierung ersetzt. Warum das zulässig ist, erfährt man hier.

(2) Konsum

Für die Haushalte werden identische homothetische Nutzenfunktionen unterstellt. Diese recht restriktive Annahme birgt entscheidende Vorteile für die Analyse des Haushaltssektors.

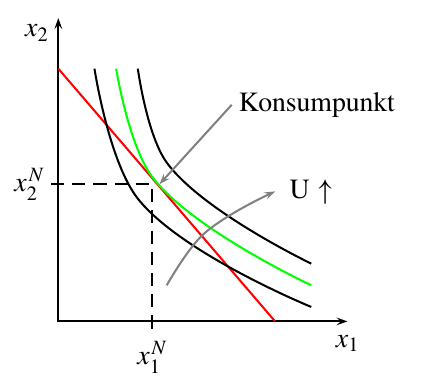
Die Einkommensverteilung (also $y_h$) spielt für die Nachfragefunktionen \[ x_1^N(p_1,p_2,y_h)\quad\text{und}\quad x_2^N(p_1,p_2,y_h) \] keine Rolle mehr. In der Tat reicht es nun aus, das Konsumverhalten eines einzelnen repräsentativen Haushalts, auf dem das gesamte Volkseinkommen vereint ist, zu untersuchen. \[ \max_{x_1,x_2}\left\{u(x_1,x_2)\ |\ p_1x_1+p_2x_2\leqq y\right\} \] Die Lösung $(x_1^N,x_2^N)$ heißt Konsumpunkt.
Gehören dem repräsentativen Haushalt sämtliche Faktorbestände $v_1$ und $v_2$, dann stimmt sein Faktoreinkommen \[ y=q_1v_1+q_2v_2 \] mit den Konsumausgaben (keine Ersparnis) \[ y=p_1x_1^N(p_1,p_2,y)+p_2x_2^N(p_1,p_2,y) \] überein. Diese Konsumausgaben entsprechen zugleich den gesamtwirtschaftlichen Erlösen. \[ y=r(p_1,p_2,v_1,v_2) \] Beachte: Die Faktoreinkommen (bzw. die Faktorkosten) und die Konsumausgaben stimmen überein. Demnach gibt es keine residualen Gewinne, was mit der Annahme linear-homogener Produktionsfunktion korrespondiert. Im langfristigen Gleichgewicht bei vollständiger Konkurrenz sind alle Gewinne wegkonkurriert.

(3) Simultanes Gleichgewicht auf allen Märkten.

Faktormärkte
Im Zuge der Erlösmaximierung hat sich die Räumung aller Faktormärkte als Optimumbedingung herausgestellt \[ v_1=v_{11}+v_{12}\quad\text{und}\quad v_2=v_{21}+v_{22} \] Dabei wird die sektorspezifische Faktornachfrage von den Faktorpreisen bestimmt. Weil die Faktorbestände annahmengemäß vollkommen preisunelastisch angeboten werden, kann nur die Faktorallokation innerhalb der Edgeworth-Box entlang der Effizienkurve variieren. Die Größe der Edgeworth-Box sowie die Menge möglicher Produktionspunkte bleiben unverändert.
Ohne die Annahme vollkommen preisunelastischer Faktorangebote würde sich eine graphische Darstellung erübrigen, weil alternative Faktorpreise immer auch alternative Transformationskurven implizieren würden.
Gütermärkte
Die für den Außenhandel wichtigeren Gütermärkte sind ausgeglichen, wenn der Produktionspunkt ($x_1^A,x_2^A$) mit dem Konsumpunkt ($x_1^N,x_2^N$) zusammenfällt. \begin{align*} x_1^A(p_1,p_2,v_1,v_2)&=x_1^N\big(p_1,p_2,\tilde r(p_1,p_2,v_1,v_2)\big)\\ x_2^A(p_1,p_2,v_1,v_2)&=x_2^N\big(p_1,p_2,\tilde r(p_1,p_2,v_1,v_2)\big) \end{align*}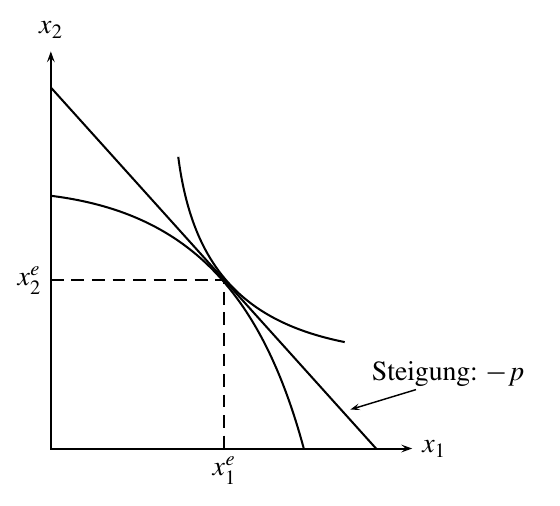

(4) Gleichgewichtige Marktpreise

In den Gleichungen für die Gütermärkte sind die nationalen Faktorbestände gegeben. Hat man gleichgewichtige Preise $p_1$, $p_2$ gefunden, so dass die Gütermärkte geräumt sind, dann sind die produzierten Gütermengen bekannt und die zugehörige Faktorallokation kann (als Punkt auf der Effizienzkurve) bestimmt werden. Damit sind schließlich auch die Faktorpreise bekannt.

Mit den beiden Gleichgewichtsbedingungen für die Gütermärkte stehen zwei Gleichungen zur Bestimmung der beiden Preise zur Verfügung. Allerdings ist zu beachten, dass

die Angebotsfunktionen homogen vom Grade 0 in den Preisen sind, d.h. \[ \mu^0 x_j^A(p_1,p_2;\cdot)=x_j^A(\mu p_1,\mu p_2;\cdot)\qquad\forall \mu>0 \] Für den Speziall $\mu=1/p_2$ und den Relativpreis $p:=p_1/p_2$ setzt man \[ x_j^A(p_1/p_2,1;\cdot)=: x_j^A(p;\cdot). \]
die Erlösfunktion homogen vom Grade 1 in den Preisen ist, d.h. \[ \mu^1 \tilde r(p_1,p_2;\cdot)=\tilde r(\mu p_1,\mu p_2;\cdot)\qquad\forall \mu>0 \] Für den Speziall $\mu=1/p_2$ setzt man \[ \tilde r(p_1/p_2,1;\cdot)=: r(p;\cdot) \]
die Nachfragefunktionen homogen vom Grade 0 in den Preisen sind, d.h. \[ \mu^0 x_j^N\big(p_1,p_2,\tilde r(p_1,p_2;\cdot)\big)=x_j^N\big(\mu p_1,\mu p_2, \tilde r(\mu p_1,\mu p_2;\cdot)\big)\qquad\forall \mu>0 \] Für den Speziall $\mu=1/p_2$ setzt man \[ x_j^N\big(p_1/p_2,1,\tilde r(p_1/p_2,1;\cdot)\big)=: x_j^N\big(p,r(p;\cdot)\big) \]

Damit wird deutlich, dass die beiden Gleichungen für die Gütermärkte nur vom Relativpreis $p$ abhängen. \begin{align*} x_1^A(p,v_1,v_2)&=x_1^N\big(p,r(p,v_1,v_2)\big)\\ x_2^A(p,v_1,v_2)&=x_2^N\big(p,r(p,v_1,v_2)\big) \end{align*} Allerdings ist eine der beiden Gleichungen redundant, denn \[ p x_1^A(p,v_1,v_2)+x_2^A(p,v_1,v_2)=r=y=px_1^N\big(p,r(p,v_1,v_2)\big)+x_2^N\big(p,r(p,v_1,v_2)\big) \] bzw. \[ p\left[x_1^N\big(p,r(p,v_1,v_2)\big)-x_1^A(p,v_1,v_2)\right]+ \left[x_2^N\big(p,r(p,v_1,v_2)\big)-x_2^A(p,v_1,v_2)\right]=0 \] zeigt, falls einer der beiden Märkte im Gleichgewicht ist, muss auch der andere Märkt geräumt sein. Diese Schlussfolgerung wird Walras Gesetz genannt.

Privatdozent Dr. Hagen Bobzin