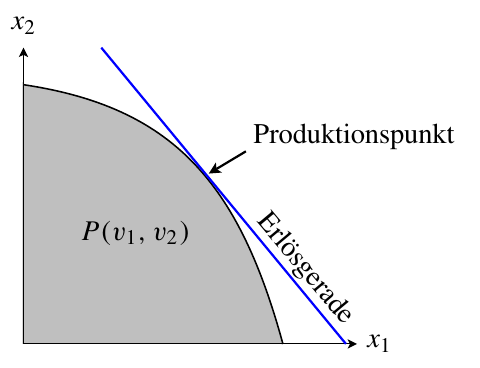
Gesamtwirtschaftliche Erlösmaximierung
Das Problem der gesamtwirtschaftlichen Erlösmaximierung bei zwei Gütern $x_1$, $x_2$ und zwei Produktionsfaktoren $v_1$, $v_2$ \[ \tilde r(p_1,p_2,v_1,v_2)=\max_{x_1,x_2}\left\{p_1x_1+p_2x_2\ |\ (x_1,x_2)\in P(v_1,v_2)\right\} \] basiert auf der Menge möglicher Produktionspunkte (Graphik), der die nationalen Faktorbeständen $v_1$ und $v_2$ sowie die sektorspezifischen Produktionsfunktionen $f_1$ und $f_2$ zugrunde liegen: \begin{align*} P(v_1,v_2):=\big\{(x_1,x_2)\geqq (0,0)\;|\;& x_j\leq f_j(v_{1j},v_{2j}),\\ & (v_{1j},v_{2j})\geqq (0,0),\ \ j=1,2;\\ & v_{i1}+v_{i2}\leq v_i,\ \ i=1,2\big\} \end{align*} Da $x_j< f_j(v_{1j},v_{2j})$ einem Erlösmaximum widerspricht, ergibt sich die folgende Lagrange-Funktion \[ \cL=p_1f_1(v_{11},v_{21})+p_2f_2(v_{12},v_{22}) +\lambda_1(v_1-v_{11}-v_{12})+\lambda_2(v_2-v_{21}-v_{22}) \] mit den notwendigen Bedingungen erster Ordnung für ein Erlösmaximum \begin{align*} (a)\quad \abl{\cL}{v_{11}}&=p_1\abl{f_1}{v_{11}}-\lambda_1=0 & (b)\quad \abl{\cL}{v_{21}}&=p_1\abl{f_1}{v_{21}}-\lambda_2=0\\ (c)\quad \abl{\cL}{v_{12}}&=p_2\abl{f_2}{v_{12}}-\lambda_1=0 & (d)\quad \abl{\cL}{v_{22}}&=p_2\abl{f_2}{v_{22}}-\lambda_2=0\\ (e)\quad \abl{\cL}{\lambda_1}&=v_1-v_{11}-v_{12}=0 & (f)\quad \abl{\cL}{\lambda_2}&=v_2-v_{21}-v_{22}=0 \end{align*} Beachte: hat man aus den sechs Gleichungen die sechs Variablen $v_{11}$, $v_{12}$, $v_{21}$, $v_{22}$, $\lambda_1$, $\lambda_2$ bestimmt, dann sind auch die Produktionsmengen $x_1$, $x_2$ bekannt. Die Bedingungen (e) und (f) verlangen die Vollbeschäftigung beider Faktoren. Die Bedingungen (a) bis (d) lassen sich zweifach interpretieren.Auf der einen Seite gilt \[ \frac{\partial f_1/\partial v_{11}}{\partial f_1/\partial v_{21}}= \frac{\partial f_2/\partial v_{12}}{\partial f_2/\partial v_{22}}= \frac{\lambda_1}{\lambda_2}. \] Demnach müssen die Grenzraten der (technischen) Substitution (GRS) in beiden Sektoren übereinstimmen \[ \text{GRS}_1=-\frac{\d v_{21}}{\d v_{11}}=-\frac{\d v_{22}}{\d v_{12}}=\text{GRS}_2, \] d.h., die entsprechenden Isoquanten tangieren einander auf der Effizienzkurve in der Edgeworth-Box (siehe Graphik). Auf der anderen Seite gilt ebenso \[ \frac{\partial f_2/\partial v_{12}}{\partial f_1/\partial v_{11}}= \frac{\partial f_2/\partial v_{22}}{\partial f_1/\partial v_{21}}=\frac{p_1}{p_2}. \] Die Interpretation der beiden linken Ausdrücke als Grenzrate der Transformation (GRT) erfordert einigen Aufwand und erfolgt extern. Es ergibt sich \[ \text{GRT}=-\frac{\d x_2}{\d x_1}=\frac{p_1}{p_2}. \] Die entsprechende Lösung im Güterraum heißt Produktionspunkt.