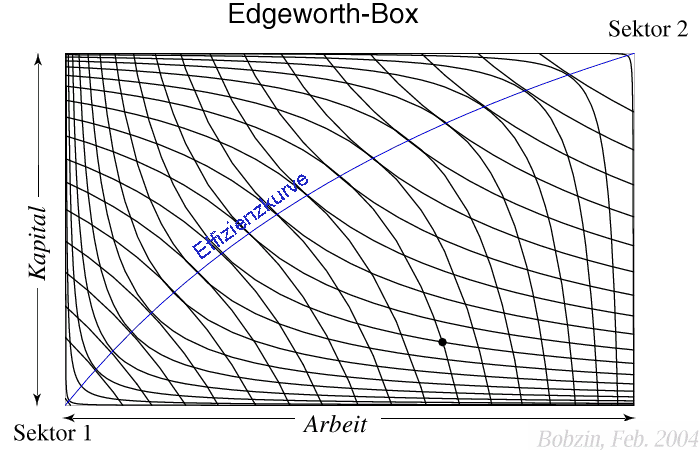
Edgeworth-Box im Faktorraum
Edgeworth-Box für zwei Produktionssektoren,
die zwei Produktionsfaktoren einsetzen:
Ziel: Suche alle
pareto-optimalen
Faktorallokationen ausgehend von gegebenen Anfangsaustattungen der Unternehmen
und bestimme die zugehörigen Ausbringungsmengen.
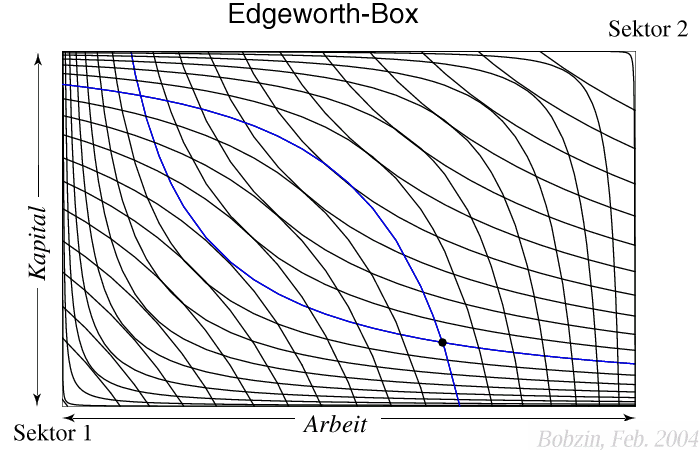
Herleitung der Tauschbox für zwei Unternehmen bzw. Sektoren, die die Güter
$x_1$ bzw. $x_2$ unter Verwendung zweier Produktionsfaktoren (Arbeit $v_1$ und
Kapital $v_2$) herstellen.
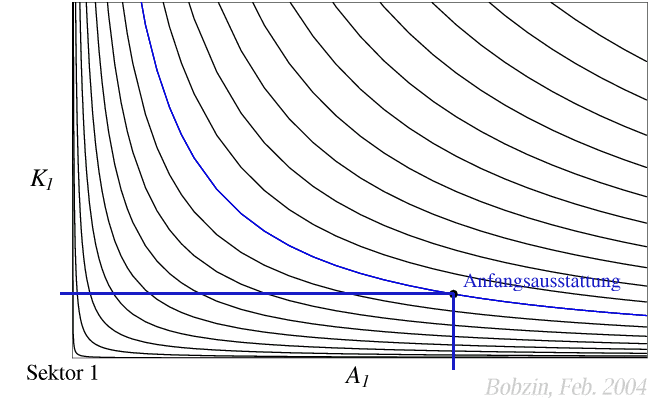
Anfangsausstattung $(v_{11},v_{21})$ des ersten Sektors, der das
Gut $x_1$ bei
fallenden Skalenerträgen
produziert.
\[
x_1 = {v_{11}}^{0,4}{v_{21}}^{0.4}
\]
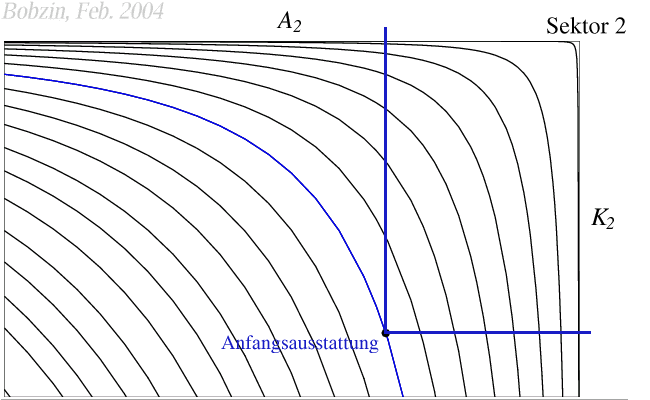
Anfangsausstattung $(v_{12},v_{22})$ des zweiten Sektors - die
Abbildung ist um 180° gedreht worden -, der das Gut $x_2$ bei
steigenden Skalenerträgen produziert.
\[
x_2 = {v_{12}}^{1}{v_{22}}^{1,5}
\]
Gesamtwirtschaftliche Faktorausstattung beider Sektoren $v_1^A =
v_{11}+v_{12}$ und $v_2^A = v_{21} + v_{22}$.
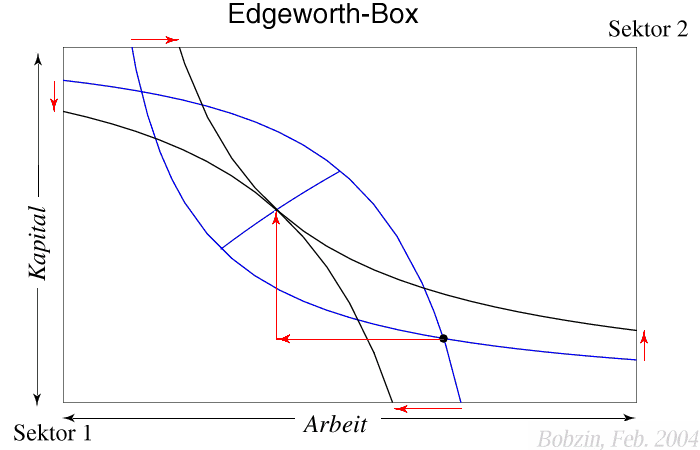
Jede Reallokation der Faktoren, die zu einer neuen Faktorallokation innerhalb
der blau umrandeten Linse führt, verbessert die Position beider Unternehmen,
weil beide ihren Output erhöhen können; man spricht auch hier von der
Tauschlinse.
Dort, wo sich die Isoquanten tangieren, gibt es keine weiteren
Tauschmöglichkeiten, die wenigstens einen Sektor besser stellen, ohne den
anderen Sektor zu benachteiligen. Diese Allokationen sind
pareto-effizient.
Der geometrische Ort aller pareto-effizienten Allokationen heißt
Effizienzkurve. Auf ihr stimmen die Grenzraten der technischen
Substitution (
GRS) überein.
Die Effizienzkurve bezeichnet pareto-effiziente Faktorallokationen und wird
daher im Faktorraum dargestellt. Die zugehörigen Ausbringungsmengen lassen
sich nun in den Güterraum übertragen, so dass man die
Transformationskurve erhält.
Tauschkurve
Edgeworth-Box (Konstruktionsprinzip)
Edgeworth-Box im Güterraum
Transformationskurve
Hauptsätze der Wohlstandstheorie
Francis Ysidro Edgeworth