Transformationskurve

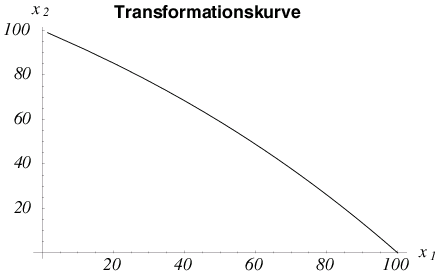
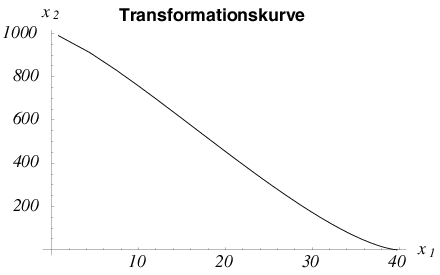
Die Transformationskurve einer Volkswirtschaft bezeichnet die maximale Gütermenge $x_2$ für eine gegebene Gütermenge $x_1$ bei gegebener Faktorausstattung (Arbeit $v_1$ und Kapital $v_2$) der Volkswirtschaft und gegebenen Produktionstechnologien (Produktionsfunktionen der Sektoren).
Ausgangspunkt ist die Effizienzkurve; sie bezeichnet pareto-effiziente Faktorallokationen und wird daher im Faktorraum dargestellt. Die zugehörigen Ausbringungsmengen lassen sich anschließend in den Güterraum übertragen, so dass man die Transformationskurve erhält. Die Steigung der Transformationskurve wird als Grenzrate der Transformation (GRT) bezeichnet.
Formal ergibt sich die Transformationskurve als "äußerer" Rand der Menge möglicher Produktionspunkte, die auf den nationalen Faktorbeständen $v_1$ und $v_2$, den sektorspezifischen Faktorallokationen $\big((v_{11},v_{21}),(v_{12},v_{22})\big)$ sowie den sektorspezifischen Produktionsfunktionen $f_1$ und $f_2$ basiert: \begin{align*} P(v_1,v_2):=\big\{(x_1,x_2)\geqq (0,0)\;|\;& x_j\leq f_j(v_{1j},v_{2j}),\\ & (v_{1j},v_{2j})\geqq (0,0),\ \ j=1,2;\\ & v_{i1}+v_{i2}\leq v_i,\ \ i=1,2\big\} \end{align*}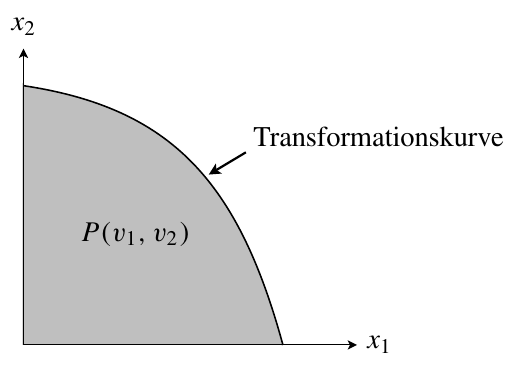
Abb. Menge möglicher Produktionspunkte
In der Regel wird die Transformationskurve mit konkavem Verlauf dargestellt. Für die beiden linear-homogenen Produktionsfunktionen \[ x_1 = {v_{11}}^{0,4}{v_{21}}^{0,6}\quad\text{und}\quad x_2 = {v_{21}}^{0,8}{v_{22}}^{0,2} \] und die Gesamtausstattung $v_1=100$ und $v_2=100$ ergibt sich folgende Abbildung.
Abb. Transformationskurve
Konkave Transformationskurven ergeben sich nicht zwingend wie die folgende Abbildung auf Basis der beiden Produktionsfunktionen \[ x_1={v_{11}}^{0,4}{v_{21}}^{0,4}\quad\text{und}\quad x_2={v_{12}}^{1}{v_{22}}^{1,5} \] und der Gesamtausstattung $v_1=100$ und $v_2=100$ zeigt.
Abb. Transformationskurve
Effizienzkurve
Hauptsätze der Wohlstandstheorie
Francis Ysidro Edgeworth No Title