Grenzrate der technischen Substitution (GRS)
(1) Ökonomisch gibt die Grenzrate der technischen Substitution (GRS) zwischen zwei Produktionsfaktoren an, um wie viele Einheiten der Produktionsfaktor v2 erhöht (gesenkt) werden muss, wenn bei gleicher Ausbringungsmenge x der Faktoreinsatz v1 "um eine Einheit" reduziert (erhöht) wird.
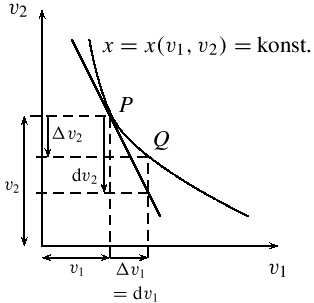
(2) Geometrisch kann man sich diese Faktorsubstitution als einen Schritt
von P nach Q entlang der Isoquante,
die zu x gehört, vorstellen.
(3) Mathematisch entspricht die GRS der Steigung einer
Isoquanten im Punkt $(v_1,v_2)$.
Bilde das totales Differential der Produktionsfunktion $x=x(v_1,v_2)$. \[ \d x =\ \abl{x(v_1,v_2)}{v_1}\ \d v_1 +\ \abl{x(v_1,v_2)}{v_2}\ \d v_2 \] Auf einer Isoquante ist $x=$ konstant, also $\d x=0$. Damit folgt durch bloße Umstellung \[ \text{GRS} = -\ \frac{\d v_2}{\d v_1} =\ \frac{\abl{x(v_1,v_2)}{v_1}}{\abl{x(v_1,v_2)}{v_2}}, \] so wie es der Satz der impliziten Differentiation besagt.
Bilde das totales Differential der Produktionsfunktion $x=x(v_1,v_2)$. \[ \d x =\ \abl{x(v_1,v_2)}{v_1}\ \d v_1 +\ \abl{x(v_1,v_2)}{v_2}\ \d v_2 \] Auf einer Isoquante ist $x=$ konstant, also $\d x=0$. Damit folgt durch bloße Umstellung \[ \text{GRS} = -\ \frac{\d v_2}{\d v_1} =\ \frac{\abl{x(v_1,v_2)}{v_1}}{\abl{x(v_1,v_2)}{v_2}}, \] so wie es der Satz der impliziten Differentiation besagt.
Grafische Darstellung:
abnehmende GRS
Outputmaximierung
Kostenminimierung
GRS Grenzrate der Substitution im Konsum
GRiS Grenzrate der intertemporalen Substitution

