Umhüllenden-Satz
Der
Umhüllenden-Satz (envelope theorem) macht eine Aussage
darüber, wie sich der Wert einer Zielfunktion verändert, wenn ein Parameter
des entsprechenden Problems variiert wird und der Entscheidungsträger simultan
die optimale Lösung an die neuen Gegebenheiten anpasst.
Umhüllenden-Satz1
Ausgangspunkt ist eine Funktion $\psi$, die für $(x,a)\in X×A$
definiert ist. Darüber hinaus definiert man die beiden Funktionen $\psi^*$ und
$x^*$ gemäß
\[
x^0=x^*(a):=\text{arg} \max_{x\in X}\, \psi(x,a)\quad\text{und}\quad
\psi^*(a)=\psi(x^*(a),a):=\max_{x\in X}\,\psi(x,a).
\]
Sind $\psi$ und $\psi^*$ stetig differenzierbar in $a$, dann gilt:
\[
\abl{\psi(x^0,a)}{a}=\frac{\d \psi^*(a)}{\d a}\,.
\]
Zur Schreibweise: Das Argument der Maximierung arg max $f(x)$
bezeichnet die Stellen $x^0$, an denen die Funktion $f$ ihr Maximum annimmt.
Der Nutzen dieses Satzes besteht darin, dass sich nun die Effekte einer
parametrischen Variation von $a$ auf die
Umhüllende $\psi^*$
erheblich einfacher berechnen lassen. Laut Kettenregel gilt nämlich
die Gleichung
\[
\frac{\d \psi^*(a)}{\d a}=
\abl{\psi(x^0,a)}{a}+\abl{\psi(x^0,a)}{x}\,\frac{\d x^*(a)}{\d a},
\]
wobei der Umhüllenden-Satz besagt, dass der letzte Ausdruck gleich null ist.
Man beachte, dass sich der Umhüllenden-Satz ohne weiteres auf viele Variablen
($x\to\vx$) und viele Parameter ($a\to\va$) anwenden lässt.
Beispiel 1: Maximiere die Funktion $\psi(x,a)=-(x-a)^2+x$ bezüglich
$x$. Also
\[
\abl{\psi(x^0,a)}{x}=-2(x-a)+1=0 \implies x^0=x^*(a)=0,5+a
\]
Und damit folgt
\[
\psi(x^0,a)=-(x^0-a)^2+x^0=-(0,5+a-a)^2+0,5+a=0,25+a=\psi^*(a)
\]
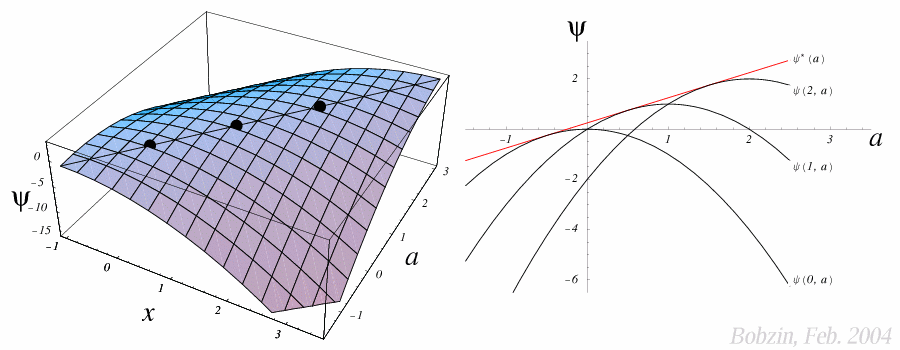
In der folgenden Abbildung ist zunächst die dreidimensionale Oberflächer der
Funktion $\psi(x,a)$ dargestellt. Die
Kurve über den Bergkamm
entspricht der dreidimensionalen Funktion $\psi(x^*(a),a)$. Übertragen in die
rechte zweidimensionale Grafik ergibt sich dieselbe Kurve als
$\psi^*(a)=0,25+a$. Diese Funktion repräsentiert die
Umhüllende der
verschiedenen $\psi(x,a)$ Kurven, von denen $\psi(0,a)$, $\psi(1,a)$ und
$\psi(2,a)$ eingezeichnet sind.
Beispiel 2: Maximiere die Funktion $\psi(x,a)=-(x-a^2)^2+x$ bezüglich $x$. Also
\[
\abl{\psi(x^0,a)}{x}=-2(x-a^2)+1=0 \implies x^0=x^*(a)=0,5+a^2
\]
Und damit folgt
\[
\psi(x^0,a)=-(x^0-a^2)^2+x^0=-(0,5+a^2-a^2)^2+0,5+a^2=0,25+a^2=\psi^*(a)
\]
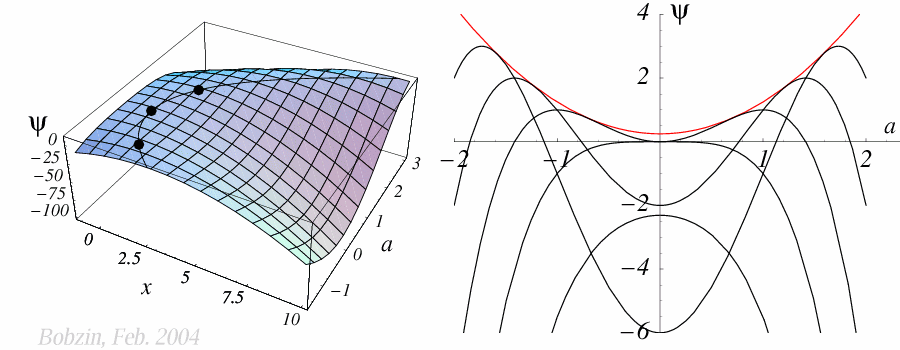
In der folgenden Abbildung ist zunächst die dreidimensionale Oberflächer der
Funktion $\psi(x,a)$ dargestellt. Die
Kurve über den Bergkamm
entspricht der dreidimensionalen Funktion $\psi(x^*(a),a)$. Übertragen in die
rechte zweidimensionale Grafik ergibt sich dieselbe Kurve als
$\psi^*(a)=0,25+a^2$. Diese Funktion repräsentiert die
Umhüllende der
verschiedenen $\psi(x,a)$ Kurven, von denen $\psi(-1.1,a)$, $\psi(0,a)$,
$\psi(1,a)$, $\psi(2,a)$ und $\psi(3,a)$ eingezeichnet sind.
Bis hierher enthalten die Optimierungsprobleme keine Restriktionen. Im Wege
des
Lagrange-Ansatzes lassen sich jedoch
sämtliche Ergebnisse auf beschränkte Optimierungsprobleme bzw. deren
Lagrange-Funktion übertragen.
Ausgangspunkt ist ein Maximierungsproblem mit dem Parameter $a$
\[
\max\{f(x,a)|\ g(x,a)\geq 0,\ x\geq 0\}
\]
Die optimale Wahl von $x$ wird mit $x^0$ bezeichnet und hängt von dem
Parameter $a$ ab,
\[
x^0=x^*(a)=\text{arg max}\{f(x,a)|\ g(x,a)\geq 0,\ x\geq 0\}\,.
\]
Der maximale Wert der Zielfunktion lautet $y^0=f(x^*(a),a)$.
Da die maximierte Funktion $f(x^*(a),a)$ (
optimum value
function) nur noch vom Parameter $a$ abhängt, erhält diese
Umhüllende einen neuen Namen
\[
y^0=f^*(a)=f(x^*(a),a)\quad\text{(Umhüllende).}
\]
Damit stellt sich die Frage, wie $y^0$ auf eine Änderung von $a$ reagiert.
\begin{equation}
\frac{\d f^*(a)}{\d a}=\abl{f(x^0,a)}{x}\frac{\d x}{\d a}+\abl{f(x^0,a)}{a}
\end{equation}
Im Folgenden wird $\partial f(x^0,a)/\partial x$ berechnet, wobei zu
berücksichtigen ist, dass die optimale Wahl von $x$, also $x^0=x^*(a)$,
simultan an den neuen Parameterwert angepasst wird. Hierzu werden die aus der
Lagrange-Funktion
\[
L(x,\lambda)=f(x,a)+\lambda g(x,a)
\]
resultierenden Kuhn-Tucker-Bedingungen benötigt.
\begin{eqnarray*}
\abl{L(x^0,\lambda^0)}{x}=&\abl{f(x^0,a)}{x}+\lambda^0\abl{g(x^0,a)}{x}\leq
0;\ \ &
x^0&\geq 0;\ \ & \abl{L(x^0,\lambda^0)}{x}x^0&=0;\\
\abl{L(x^0,\lambda^0)}{\lambda}=&g(x^0,a)\geq 0;\ \ &
\lambda^0&\geq 0;\ \ & \abl{L(x^0,\lambda^0)}{\lambda}\lambda^0&=0.
\end{eqnarray*}
Die letzte Bedingung besagt nichts anderes als $\lambda^0g(x^0,a)\equiv
\lambda^*(a)\cdot g(x^*(a),a)=0$, so dass im Optimum
\[
L^*(a)\equiv L(x^*(a),\lambda^*(a))=
L(x^0,\lambda^0)=f(x^0,a)=f(x^*(a),a)\equiv f^*(a)
\]
erfüllt sein muss. Bei einer
inneren Lösung, d.h. $x^0>0$,
verlangt die erste Zeile der Kuhn-Tucker-Bedingungen
\[
\abl{f(x^0,a)}{x}=-\lambda^0\abl{g(x^0,a)}{x}.
\]
Weil der Fall $\lambda^0=0$ unmittelbar $\partial f(x^0,a)/\partial x=0$
impliziert, wird nun $\lambda^0=\lambda^*(a)>0$ unterstellt, so dass
\[
g(x^0,a)=0 \implies \abl{g(x^0,a)}{x}\d x+\abl{g(x^0,a)}{a}\d a=0.
\]
Damit erhält man
\[
\abl{f(x^0,a)}{x}=\lambda^0\abl{g(x^0,a)}{a}\frac{\d a}{\d x}
\quad\text{oder}\quad
\abl{f(x^0,a)}{x}\frac{\d x^*(a)}{\d a}=\lambda^0\abl{g(x^0,a)}{a}.
\]
Mit diesem Ergebnis wird (1) zu
\[
\frac{\d f^*(a)}{\d a}=\abl{f(x^0,a)}{a}+\lambda^0\abl{g(x^0,a)}{a}
\]
Der Umhüllenden-Satz besagt demnach, dass man $x^0=x^*(a)$ bei
der Ableitung der Umhüllenden $f^*(a)=f(x^*(a),a)$ nach dem Parameter $a$ wie
eine Konstante behandeln darf.
Achtung: Bei einer Ecklösung mit $x^0=0$ und
\[
\abl{f(x^0,a)}{x}<\lambda^0\abl{g(x^0,a)}{x}
\]
trifft die Aussage des Umhüllenden-Satzes nicht zu.
Shephards Lemma
Roys Identität,
Beweis
Wolds Theorem,
Beweis
Lagrange-Multiplikator: Grenznutzen des Geldes
Lagrange-Multiplikator
Lagrange-Multiplikator: Grenzertrag des Geldes
Lagrange-Multiplikator
Footnotes:
1Die exakte Form findet man in Feichtinger und
Hartl (1986), S. 34 oder Varian (1989), S. 336 ff.