Skalenerträge (returns to scale)
Skalenerträge messen, wie sich das Outputniveau $x$ verändert, wenn sämtliche
Produktionsfaktoren $\vv$ um denselben Faktor $\lambda$
variiert werden (
totale Faktorvariation).
Da alle Faktoren skaliert werden, lässt sich das Konzept nur schwerlich mit
fixen Produktionsfaktoren in Einklang bringen.
steigende Skalenerträge
(economies of scale, vgl. überlinearhomogene Produktionsfunktionen)
\[
\lambda x(\vv) < x(\lambda \vv)\qquad\forall\ \lambda>1
\]
konstante Skalenerträge
(vgl. linearhomogene Produktionsfunktionen)
\[
\lambda x(\vv) = x(\lambda \vv)\qquad\forall\ \lambda>0
\]
fallende Skalenerträge
(diseconomies of scale, vgl. unterlinearhomogene Produktionsfunktionen)
\[
\lambda x(\vv) > x(\lambda \vv)\qquad\forall\ \lambda>1
\]
Niveauproduktionsfunktion
resultierende Eigenschaften der Kostenfunktion
Verbundvorteile (economies of scope)
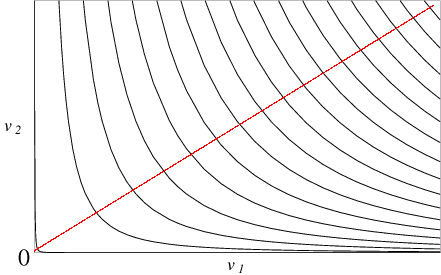
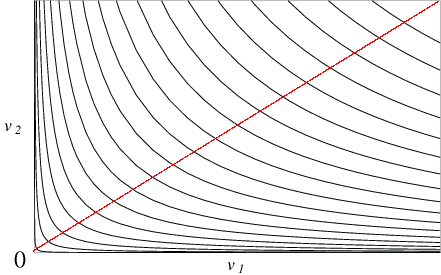
Bei steigenden Skalenerträgen nimmt der Abstand zwischen den Isoquanten
aufgrund des unterproportional steigenden Faktorbedarfs ab.
Bei fallenden Skalenerträgen nimmt der Abstand zwischen den Isoquanten
aufgrund des überproportional steigenden Faktoreinsatzes zu.