Nachfragekurve
Zur analytischen Herleitung der Marschallschen Funktionen der Güternachfrage ist das Problem der Nutzenmaximierung zu lösen. Die analogen Hicksschen Funktionen ergeben sich aus der Ausgabenminimierung. Für die grafische Ableitung der Nachfragekurve x1 = x1(p1) geht man von einem Haushaltsoptimum aus. Für p1' ist das der unterste Tangentialpunkt im oberen Teil der folgenden Grafik. Nun erhöht man sukzessive den Preis auf p1" und dann auf p1"', so dass sich die Budgetgerade nach oben dreht. Gleichzeitig stellen sich neue Tangentialpukte als Haushaltsoptima ein (siehe Preis-Konsum-Kurve). Für jeden Preis (p1', p1"' und p1"') kann man nun die nachgefragte Menge des ersten Gutes ablesen und in die untere Grafik übertragen.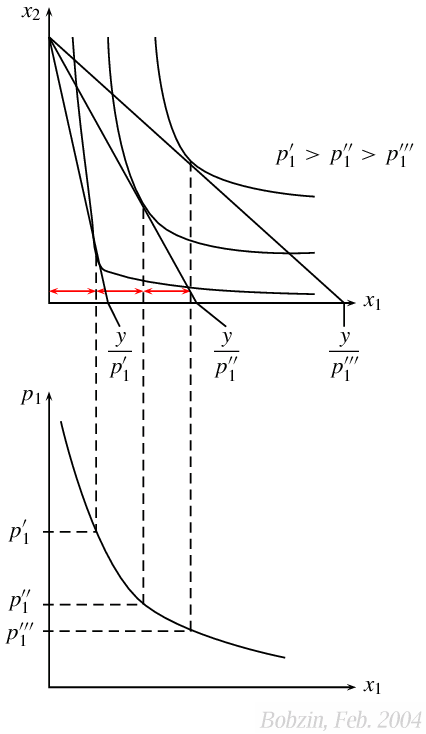
Das gleiche Prinzip lässt sich nicht nur auf das zweite Gut anwenden, man kann
alternativ auch den Preis p2, das Einkommen y (siehe
Einkommen-Konsum-Kurve) oder andere Parameter
variieren.
Marschallsche Funktionen der GüternachfrageHickssche Funktionen der Güternachfrage