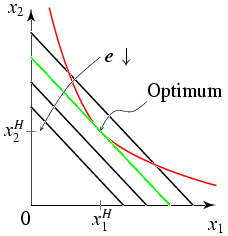
Hickssche Nachfragefunktionen
Die
Ausgabenminimierung generiert die
Hicksschen
oder kompensierten Nachfragefunktionen
\[
x_1^*=x_1^H(p_1, p_2, U) \UND x_2^*=x_2^H(p_1, p_2, U);
\]
Diese Funktionen sind
homogen vom Grade null in p1 und
p2. Zum Beweis dieser Aussage wird die entsprechende Lagrange-Funktion
herangezogen, wobei die Preise mit dem Faktor
k
multipliziert werden.
\[
\cL(x_1,x_2,\lambda) = (k p_1)x_1 + (k p_2)x_2 + \lambda (U-u(x_1, x_2) )
\]
Der Faktor
k tritt nur in den ersten beiden Lagrange-Bedingungen
\begin{eqnarray*}
\abl{\cL}{x_1} &=& k p_1-\lambda^*\abl{u(x_1^*,x_2^*)}{x_1} = 0\\
\abl{\cL}{x_2} &=& k p_1-\lambda^*\abl{u(x_1^*,x_2^*)}{x_2} = 0\\
\abl{\cL}{\lambda} &=& U=u(x_1^*,x_2^*) = 0
\end{eqnarray*}
auf. Dividiert man die ersten beiden Gleichungen durcheinander, dann spielt
k keine Rolle mehr und es ergibt sich
dieselbe Grenzrate der Substitution (
GRS) wie für $k=1$.
\[
\text{GRS} = \frac{{\partial}u/{\partial}x_1}{{\partial}u/{\partial}x_2} =\frac{p_1}{p_2}
\]
Setzt man die Hicksschen Funktionen in die Zielfunktion $p_1x_1+p_2x_2$ ein, so
resultiert die
Ausgabenfunktion.
Falls nur die Ausgabenfunktion bekannt ist, dann lassen sich die
Hicksschen Nachfragefunktionen mit Hilfe von
Shephards Lemma berechnen.
Marshallsche Güternachfrage