$\def\abl#1#2{\frac{\partial #1}{\partial #2}}\def\d{\textrm{d}}$

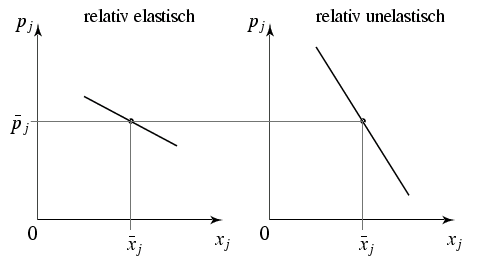
Der Begriff der Elastizität

Unter einer Elastizität versteht man immer das Verhältnis zweier relativer Änderungen
relative (prozentuale) Veränderung der abh. Var.
relative (prozentuale) Veränderung der unabh. Var.
Gemessen wird demnach die relative Auswirkung in Bezug auf die jeweilige Ursache. \[ \frac{\text{Auswirkung/Folge}}{\text{Ursache}} \] Allgemein gilt für $y = f(x)$ \begin{eqnarray*} \text{Punktelastizität; Differentialquotient}\ &&\eta =\ \frac{\d y/y}{\d x/x}\ =\ \frac{\d y}{\d x} \frac{x}{y}\\ \text{Kurvenelastizität; Differenzenquotient}\ &&\eta =\ \frac{\Delta y/y}{\Delta x/x}\ =\ \frac{\Delta y}{\Delta x} \frac{x}{y} \end{eqnarray*}
  1. Die Elastizität in einem gegebenen Punkt macht eine Aussage darüber, wie steil (oder elastisch) die Kurve verläuft: $\d y/\d x$.
    Abb. Elastizität
  2. Bewegt man den Punkt entlang einer Kurve ( →  $x/y$, dann ändert sich die Elastizität in der Regel, selbst wenn die Steigung konstant ist.
    Abb. Elastizität
  3. Die Kurve $y = a x^\alpha$ hat in jedem Punkt dieselbe Elastizität $\alpha$. \[ \eta_{yx} =\ \frac{\d y}{\d x} \frac{x}{y}\ = a \alpha x^{\alpha-1} \frac{x}{a x^\alpha}\ = \alpha \]
Einige wichtige Beispiele für Elastizitäten
Haushaltstheorie:
Als Ausgangspunkt dient die allgemeine Nachfragefunktion $x_j^M(p_1,p_2,y)$ mit $j = 1,2$.
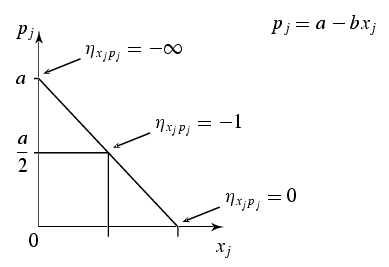
  1. Direkte Preiselastizität, Eigenpreiselastizität oder Elastizität der Nachfrage nach dem Gut $j$ in Bezug auf den eigenen Preis $p_j$ \[ \eta_{x_j p_j}\ =\ \frac{\d x_j /x_j}{\d p_j /p_j} \ =\ \frac{\d x_j}{\d p_j}\ \frac{p_j}{x_j} \]
  2. Kreuzpreiselastizität oder Elastizität der Nachfrage nach dem Gut $j$ in Bezug auf den Preis $p_k$ eines anderen Gutes ($j\ne k$) \[ \eta_{x_j p_k}\ =\ \frac{\d x_j /x_j}{\d p_k /p_k} \ =\ \frac{\d x_j}{\d p_k}\ \frac{p_k}{x_j} \]
  3. Einkommenselastizität oder Elastizität der Nachfrage nach dem Gut $j$ in Bezug auf das Einkommen $y$ \[ \eta_{x_j y}\ =\ \frac{\d x_j /x_j}{\d y /y} \ =\ \frac{\d x_j}{\d y}\ \frac{y}{x_j} \]
Theorie der Unternehmung:
  1. Gewinnmaximales Güterangebot: $x(p,q_1,q_2)$
    1. Elastizität des Angebots in Bezug auf den eigenen Preis $p$ \[ \eta_{x p} =\ \frac{\d x /x}{\d p /p}\ =\ \frac{\d x}{\d p}\ \frac{p}{x} \]
    2. Elastizität des Angebots in Bezug auf den Preis $q_i$ des Faktors $i$ \[ \eta_{x q_i} =\ \frac{\d x /x}{\d q_i /q_i}\ =\ \frac{\d x}{\d q_i}\ \frac{q_i}{x} \]
  2. Gewinnmaximale Nachfrage nach Produktionsfaktoren $v_i^M(q_1,q_2,p)$ mit $i=1,2$
    1. Elastizität der Nachfrage nach dem Faktor $i$ in Bezug auf den eigenen Preis $q_i$ \[ \eta_{v_i q_i} =\ \frac{\d v_i /v_i}{\d q_i /q_i}\ =\ \frac{\d v_i}{\d q_i}\ \frac{q_i}{v_i} \]
    2. Elastizität der Nachfrage nach dem Faktor $i$ in Bezug auf den Preis $q_k$ eines Produktionsfaktors ($i\ne k$) \[ \eta_{v_i q_k} =\ \frac{\d v_i /v_i}{\d q_k /q_k} \ =\ \frac{\d v_i}{\d q_k}\ \frac{q_k}{v_i} \]
    3. Elastizität der Nachfrage nach dem Faktor $i$ in Bezug auf den Preis $p$ des angebotenen Gutes \[ \eta_{v_i p} =\ \frac{\d v_i /v_i}{\d p /p}\ =\ \frac{\d v_i}{\d p}\ \frac{p}{v_i} \]
  3. Niveauelastizität, Skalenelastizität oder Elastizität des Outputs $x$ in Bezug auf das Produktionsniveau $\lambda$ \[ \eta_{x \lambda} =\ \frac{\d x /x}{\d \lambda /\lambda} \ =\ \frac{\d x}{\d \lambda}\ \frac{\lambda}{x} \] Niveauproduktionsfunktion
  4. Faktorelastizität, Produktionselastizität oder Elastizität des Outputs $x$ in Bezug auf den Produktionsfaktor $v_i$ \[ \eta_{x v_i} =\ \frac{\d x /x}{\d v_i /v_i} \ =\ \frac{\d x}{\d v_i}\ \frac{v_i}{x} \]
  5. Substitutionselastizität: Maß für die Krümmung einer Isoquante.