Der optimale Verbrauchsplan: Analytische Bestimmung
Kostenminimierung
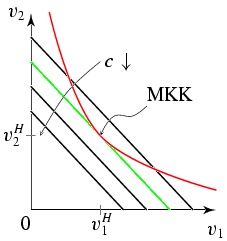
ökonomisches PrinzipDuales Problem Problem der Minimierung der Kosten $q_1v_1+q_2v_2$ unter der Nebenbedingung (Produktionsfunktion), dass mindestens das Outputniveau x realisiert werden soll (Nebenbedingung als Ungleichung). \begin{eqnarray*} &&q_1v_1 + q_2v_2\to \text{Min.}\\ \text{u.d.NB.}\quad &&x\leq x(v_1,v_2) \\ &&v_1, v_2\geq 0 \end{eqnarray*} Grafische Darstellung der Lösung:
Parameter: $q_1$, $q_2$, $x$ sind zunächst als Konstante zu behandeln.
Entscheidend: $\cL$ nimmt in Bezug auf $v_1$, $v_2$ das Minimum dort an, wo
auch die Zielfunktion minimal ist (und umgekehrt).
Kuhn-Tucker-Bedingungen:
Notwendige Bedingungen 1. Ordnung (3 Gleichungen, 3 Variablen)
\begin{eqnarray*}
\abl{\cL}{v_1} &\geq 0, && v_1^*\geq 0, && \abl{\cL}{v_1} v_1^*=0,\\
\abl{\cL}{v_2} &\geq 0, && v_2^*\geq 0, && \abl{\cL}{v_2} v_2^*=0,\\
\abl{\cL}{\lambda} &\leq0, && \lambda^*\geq0, && \abl{\cL}{\lambda}\lambda^*=0
\end{eqnarray*}
Unterstellt man eine innere Lösung, also $v_1^*>0$ und $v_2^*>0$, dann muss
\begin{eqnarray*}
\abl{\cL}{v_1} &= q_1-\lambda^*\abl{x(v_1^*,v_2^*)}{v_1} = 0\\
\abl{\cL}{v_2} &= q_2-\lambda^*\abl{x(v_1^*,v_2^*)}{v_2} = 0
\end{eqnarray*}
erfüllt sein. Nun lässt sich $\lambda^*$ eliminieren
\[
\frac{{\partial}x/{\partial}v_1}{{\partial}x/{\partial}v_2} =\frac{q_1}{q_2}
\ODER
\frac{{\partial}x/{\partial}v_1}{q_1}= \frac{{\partial}x/{\partial}v_2}{q_2}=\frac{1}{\lambda^*}
\]
Folglich muss bei positiven Grenzproduktivitäten auch $\lambda^*>0$ gelten, so
dass
\[
\abl{\cL}{\lambda} = x-x(v_1^*, v_2^*)=0
\]
Fazit: Bei positiven Gütermengen, verhalten sich die
Grenzproduktivitäten wie die Faktorpreise. Oder äquivalent, Gleichheit
des Grenzertrags des Geldes $= 1/\lambda^*$.
Nachdem $\lambda^*$ eliminiert worden ist, liegen 2 Gleichungen mit 2 Variablen
(nämlich $v_1^*$ ,$v_2^*$) vor:
\begin{eqnarray*}
\text{GRS}=\frac{{\partial}x/{\partial}v_1}{{\partial}x/{\partial}v_2}&&=-\frac{\d v_2}{\d v_1}=\frac{q_1}{q_2}.\\
x&&=x(v_1^*,v_2^*)
\end{eqnarray*}
Die zweite Bedingung beschreibt einen Punkt auf der Isoquante. Gemäß der ersten
Bedingung tangieren sich Kostengerade und Isoquante. Die Steigung der
Isoquante ist die GRS.
Beachte: Mit den Kuhn-Tucker-Bedingungen werden auch Ecklösungen erfasst, in
denen entweder $v_1^*=0$ oder $v_2^*=0$ gilt. In diesem Fall liegt keine
Tangentiallösung mehr vor.
Aufgrund der Eigenschaften der Nutzenfunktion
(abnehmende GRS) und
der Zielfunktion (konstante Güterpreise) liefert das Gleichungssystem
- die optimalen Gütermengen oder Faktornachfragefunktionen \[ v_1^*=v_1^H(q_1,q_2,x) \UND v_2^*=v_2^H(q_1,q_2,x) \]
- den optimalen Wert des Lagrange-Multiplikators $\lambda^*=\lambda(q_1,q_2,x)$. (ökonomische Interpretation)

