Grenzrate der Transformation (GRT)
Für die Erklärung des Begriffs Grenzrate der Transformation (GRT) ist vorauszusetzen, dass das Konstruktionsprinzip der Transformationskurve bzw. der Transformationsfunktion bekannt sind.
Die Transformationsfunktion einer Volkswirtschaft (hier in impliziter Form)
\[
t(x_1,x_2)=0
\]
bezeichnet die maximale Gütermenge $x_2$ für eine gegebene Gütermenge $x_1$
bei gegebener Faktorausstattung (Arbeit und Kapital) der Volkswirtschaft und
gegebenen Produktionstechnologien (Produktionsfunktionen der Sektoren).
Analytisch ergibt sich nun die Grenzrate der Transformation an der Stelle
(x1,x2) mit Hilfe des Satzes der impliziten
Differentiation
\[
\frac{\d x_2}{\d x_1}\ =\ -\ \frac{\partial t(x_1,x_2)/\partial x_1}{\partial t(x_1,x_2)/\partial x_2}
\]
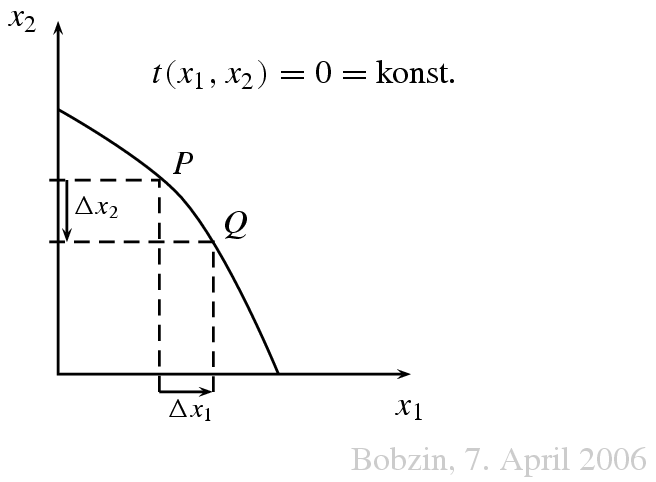
Geometrisch handelt es sich also um die Steigung der Transformationskurve.
Aus ökonomischer Sicht gibt der Ausdruck an, auf wie viele Einheiten von x2
man verzichten muss, wenn man ein zusätzliche (infinitesimal kleine) Einheit
von x1 erzeugen will. Diese Bewegung von P nach Q auf der
Transformationskurve wird durch eine Tangente im Ausgangspunkt P
approximiert.
Die Grenzrate der Transformation entspricht der Grenzrate der Substitution
(GRS) im Konsum.