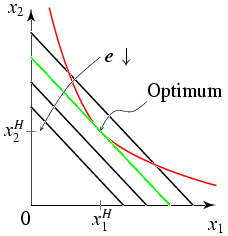
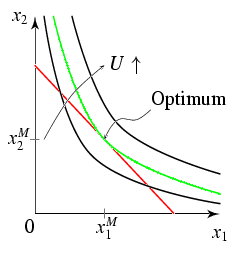
Vergleich der Hicksschen und der Marshallschen Lösung
Hickssche Güternachfrage
\[
x_j^H(\vp, U)\MIT j=1\BIS n
\]
Marschallsche Güternachfrage
\[
x_j^M(\vp, y)\MIT j=1,...,n
\]
Im Haushaltsoptimum stimmen die Hicksschen und die Marshallschen Mengen
überein
\[
x_j^*=x_j^H(\vp, U)=x_j^M(\vp, y) \MIT j=1\BIS n
\]
Im Optimum lässt sich das Nutzenniveau mit Hilfe der indirekten
Nutzenfunktion angeben, $U=v(\vp,y)$, so dass
\[
x_j^H\left(\vp, v(\vp, y) \right) = x_j^M(\vp, y)\MIT j=1\BIS n
\]
Analog können die Ausgaben im Optimum über die Ausgabenfunktion bestimmt
werden, $y=e(\vp, U)$, so dass
\[
x_j^M(\vp, e(\vp, U) ) = x_j^H(\vp, y) \MIT j=1\BIS n
\]
Slutzky Zerlegung (Details)
ökonomisches Prinzip