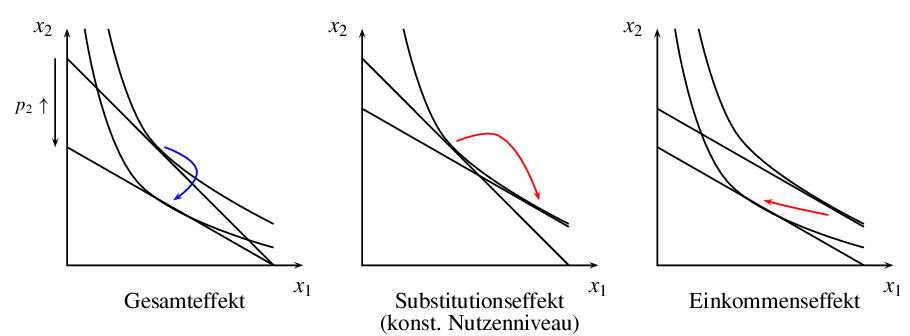
Slutzky-Zerlegung (grafisch)
Die Slutzky-Zerlegung (analytisch) \[ \abl{x_j^M(\vp, y)}{p_j}=\abl{x_j^H(\vp, U)}{p_j} - \abl{x_j^M(\vp, y)}{y} x_j^H(\vp, U) \quad\text{mit}\quad j=1,...,n \] beschreibt Preiseffekte auf die Marschallsche Güternachfrage (Gesamteffekt). Dieser Gesamteffekt setzt sich aus einem direkten und einem indirekten Preiseffekt zusammen.- Der direkte Preiseffekt passt implizit das Einkommen so an, als ob das alte Nutzenniveau $U$ konstant gehalten werden kann. Der entsprechende Substitutionseffekt ergibt sich aus der Hicksschen Faktornachfrage $x_j^H(\vp,U)$.
- Der korrigierende Einkommenseffekt
reduziert das imaginär höhere Einkommen wieder auf seinen tatsächlichen
Wert $y$, so dass nun für das neue (hier niedrigere) Nutzenniveau wieder
$y=e(\vp,U)$ gilt.
Der Einkommenseffekt kann daher als gutes Maß herangezogen werden, wie
groß die finanzielle Entschädigung eines Haushalts sein muss, damit der
Haushalt eine Preiserhöhung (z.B. durch eine Steuer) akzeptiert.
Vgl. hierzu die Ausführungen zur metrischen Nutzenfunktion.
Giffen-Gut
inferiores Gut
Metrische Nutzenfunktion

