Niveauproduktionsfunktion
Ausgangspunkt ist eine gegebene Produktionsaktivität $x^K$, $v_1^K$ ,...,
$v_m^K$ mit
\[
x^K=x(v_1^K,...,v_m^K)
\]
Diese Aktivität entspricht dem Produktionsniveau $\lambda=1$. Wird nun das
Produktionsniveau $\lambda$ erhöht, d.h.
\[
(v_1^K,...,v_n^K) \to (\lambda v_1^K,...,\lambda v_m^K),
\]
dann stellt sich die Frage, wie der Output $x^K$ reagiert. Damit liegt es
nahe, die
Niveauproduktionsfunktion $x$ als Funktion von
$\lambda$ zu definieren.
Falls die Produktionsfunktion homogen vom Grade $r$ ist, dann steigt der
Output $x$ um das $\lambda^r$-fache.
\[
\lambda^r x^K=\lambda^r x(v_1^K,...,v_n^K)=x(\lambda v_1^K,...,\lambda v_m^K)
\]
Die Niveauproduktionsfunktion lautet in diesem Fall
\[
x(\lambda)=\lambda^r x^K.
\]
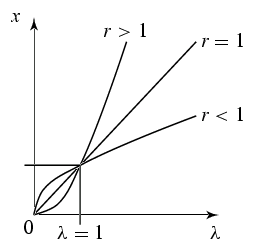
Die
Niveauleastizität gibt an, wie sich der Output prozentual
ändert, wenn das Produktionsniveau λ um einen bestimmten Prozentsatz
verändert wird.
\[
\eta_{x \lambda}=\frac{\d x /x}{\d \lambda /\lambda}
=\frac{\d x}{\d \lambda} \frac{\lambda}{x}
\]
Ist die Produktionsfunktion homogen vom Grade $r$, dann stimmt die
Niveauleastizität mit dem Homogenitätsgrad überein:
\[
\eta_{x \lambda}=r
\]
Beweis
\[
\eta_{x \lambda}
=\frac{\d x}{\d \lambda} \frac{\lambda}{x}
=r \lambda^{r-1}x^K \frac{\lambda}{\lambda^r x^K}=r
\]
Das
Wicksell-Johnson-Theorem besagt, dass
die Niveauelastizität $\eta_{x\lambda}$ generell mit der Summe der
Faktorelastizitäten übereinstimmt.
Skalenerträge


