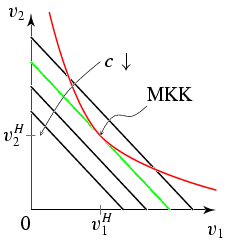
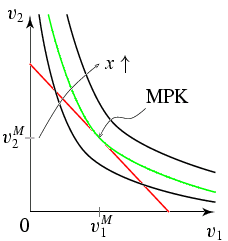
Vergleich der MKK mit der MPK
Minimalkostenkombination (MKK)
\[
v_i^H(\vq, x)\MIT i=1\BIS m
\]
Maximalproduktkombination (MPK)
\[
v_i^M(\vq, c)\MIT i=1\BIS m
\]
Im Optimum stimmt die MKK mit der MPK überein,
\[
v_i^*=v_i^H(\vq, x)=v_i^M(\vq, c) \MIT i=1\BIS m
\]
Im Optimum lässt sich die produzierte Menge über die indirekte
Produktionsfunktion ausdrücken, $x=z(\vq, c)$, so dass
\[
v_i^H\left(\vq, z(\vq, c) \right) = v_i^M(\vq, c)\MIT i=1\BIS m
\]
Analog könne die Kosten im Optimum mit Hilfe der Kostenfunktion bestimmt
werden, $c=c(\vq, x)$, so dass
\[
v_i^M(\vq, c(\vq, x) ) = v_i^H(\vq, x) \MIT i=1\BIS m
\]
ökonomisches Prinzip
Slutzky Zerlegung