Tauschkurven und Konkurrenzgleichgewicht
Ausgangspunkt ist das mikroökonomische Totalmodell mit zwei Haushalten $A$ und $B$ sowie zwei Gütern $x_1$ und $x_2$. Die Anfangsausstattungen $(w_{1A}, w_{2A})$ und $(w_{1B}, w_{2B})$ der beiden Haushalte sind gegeben. Die Herleitung der Tauschlinse sowie der Kontraktkurve als geometrischer Ort aller Pareto-effizienten Güterallokationen sollte bekannt sein.
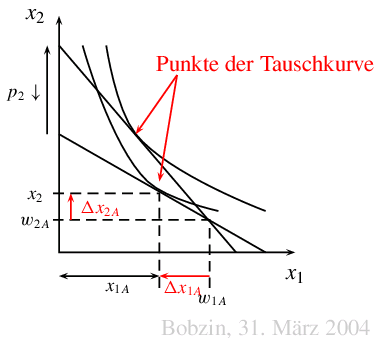
Tauschkurven beschreiben Haushaltsoptima in Abhängigkeit von dem
Güterpreisverhältnis $p=p_1/p_2$, sowie die implizierten Tauschwünsche
des betrachteten Haushalts, also $\Delta x_{1A}<0$ (Nettoangebot) und
$\Delta x_{2A}>0$ (Nettonachfrage) für den Haushalt $A$.
Formal muss Haushalt $A$ das folgende Problem der Nutzenmaximierung lösen
\[
\max\left\{u_A(x_{1A},x_{2A})\ |\ p x_{1A} + x_{2A} = p w_{1A} + w_{2A}\right\}.
\]
Das Budget wird also durch den Wert der Anfangsausstattung beschrieben.Die beiden Optimumbedingungen \[ \text{GRS}=\frac{\displaystyle\abl{u_A}{x_{1A}}}{\displaystyle\abl{u_A}{x_{2A}}}=p \quad\text{und}\quad p( x_{1A}-w_{1A}) + (x_{2A}-w_{2A}) = 0 \] liefern den Konsumpunkt $(x_{1A}^N,x_{2A}^N)$,
- der auf der zu $p$ gehörenden Budgetgeraden liegt und
- der einen Tangentialpunkt zwischen dieser Budgetgeraden und der entsprechenden Indifferenzkurve kennzeichnet.
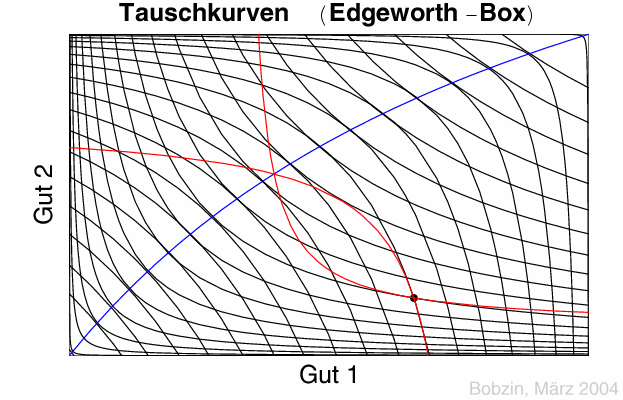
- der Tausch für beide Haushalte vorteilhaft ist (die Lösung also in der durch blaue Indifferenzkurven gekennzeichneten Tauschlinse liegt);
- die gegenseitigen Tauschvorschläge zueinander kompatibel sind
(Schnittpunkt der Tauschkurven, d.h., was der eine anbietet, fragt der andere
nach und GRS$_A=p=$GRS$_{B}$) und
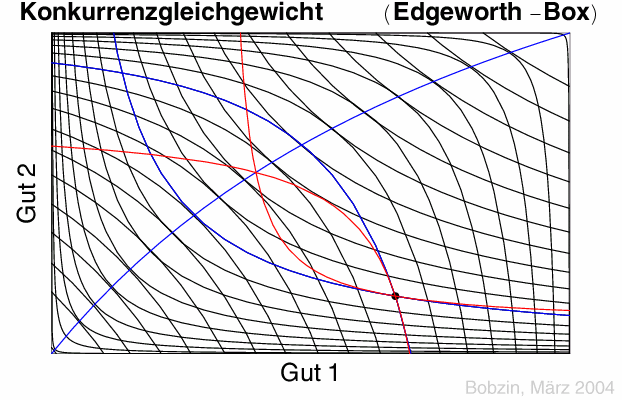
- wenn die Budgetrestriktionen eingehalten werden. \begin{eqnarray*} && p x_{1A} + x_{2A} = p w_{1A} + w_{2A} \\ && p x_{1B} + x_{2B} = p w_{1B} + w_{2B} \end{eqnarray*}
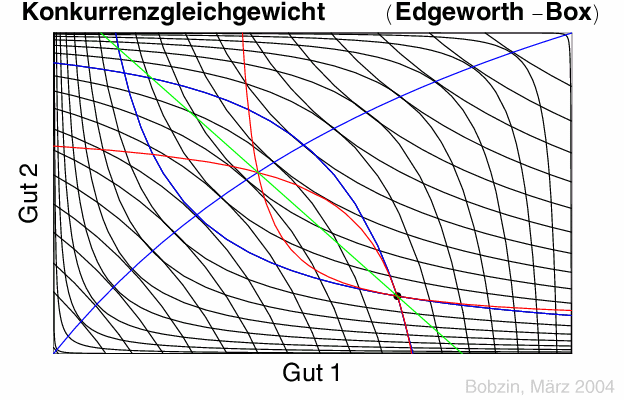
Tauschlinse
Walras-Gesetz
Edgeworth-Box (Konstruktionsprinzip)

