Begriff der Produktivität
Ausgangspunkt ist die
Produktionsfunktion
\[
x = x(v_1, v_2),
\]
wobei die Produktivität allgemein die Ergiebigkeit der Produktionsfaktoren
misst.
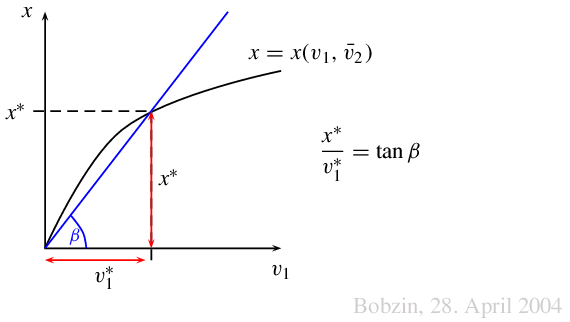
Die
Durchschnittsproduktivität des Produktionsfaktors $i$
\[
\frac{x(v_1, v_2)}{v_i}>0 \quad\text{mit}\ \ i=1, 2
\]
gibt den Output $x$ pro eingesetzte Einheit des Faktors $i$ an.
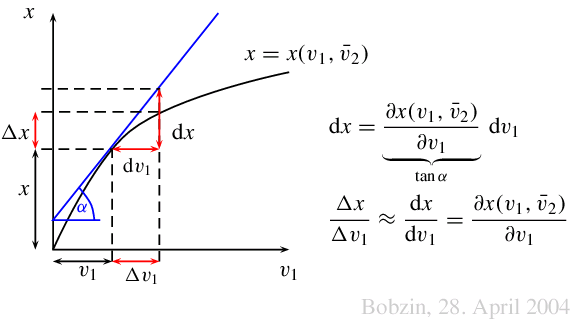
Die (physische)
Grenzproduktivität des Produktionsfaktors $i$
\[
\abl{x(v_1, v_2)}{v_i}>0 \quad\text{mit}\ \ i=1, 2
\]
gibt an, wie sich der Output $x$ verändert, wenn die eingesetzte Faktormenge
$v_i$ marginal erhöht wird. Unter Berücksichtigung der Dimensionen ist die
Grenzproduktivität vom
Grenzprodukt zu unterscheiden
\[
\d x = \abl{x(v_1, v_2)}{v_i} \d v_i \quad\text{mit}\ \ i=1, 2
\]
Die
monetäre Grenzproduktivität des Produktionsfaktors $i$
\[
p \abl{x(v_1, v_2)}{v_i}>0
\]
beschreibt, wie sich der Erlös des Unternehmens bei einem konstanten
Güterpreis $p$ verändert, wenn die Menge des Faktor $i$ marginal erhöht wird.
Gewinnmaximierung