Komparative Kostenvorteile
Ausgangspunkt ist die Frage, warum es sich für zwei Produzenten lohnt, sich zu
spezialisieren und dann Handel aufzunehmen. Die folgende Argumentation gilt
vollkommen analog für zwei Personen (hier Robinson und Freitag) wie auch für
Volkswirtschaften. Dabei ist ausdrücklich zu betonen, dass die Argumentation
nicht auf Vorteilen durch technischen Fortschritt basiert. Solche zusätzlichen
Effekte können die Gewinne aus Handel noch weiter erhöhen.
Im "Modell" stellen zwei Personen, nämlich Robinson und Freitag, jeweils
zwei Güter - Kleidung und Nahrung - her. Angenommen, Robinson benötigt 10
Stunden (Arbeitseinheiten) für die Herstellung eines Kleidungsstückes und 11
Stunden je Einheit Nahrungsmittel (z.B. je Sack Kartoffeln). Analog wird für
Freitag unterstellt, dass er 14 Stunden je Kleidungsstück und 12 Stunden je
Nahrungseinheit benötigt. Wenn beide 50 h pro Woche arbeiten, so stellt sich
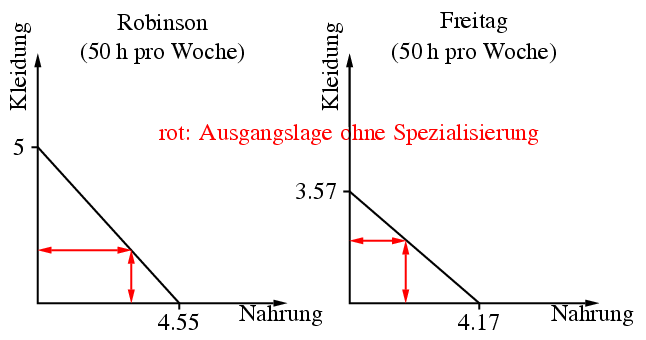
eine Ausgangssituation ein, die in der folgenden Abbildung dargestellt wird.
Links wird der wöchentliche Output anhand der entsprechenden
Transformationskurve für Robinson
abgebildet. Die roten Pfeile zeigen an, wieviel er von den beiden Gütern
produziert und konsumiert. Die rechte Grafik gilt analog für Freitag.
Absolute Kostenvorteile.
Man beachte, dass Robinson sowohl Kleidung als
auch Nahrung in kürzerer Zeit herstellen kann. Er besitzt also in beiden
Produktionsrichungen einen absoluten Kostenvorteil, wobei die Kosten in
Arbeitsstunden gemessen werden.
Warum sollte es also für den "überlegenen" Robinson vorteilhaft sein, sich
mit Freitag auf irgendeine Form der Arbeitsteilung zu einigen? Hat auch
Freitag Vorteile von einer solchen Spezialisierung? Die Antwort lautet
eindeutig "ja", wenn sich beide einen Handelsgewinn sichern können, auch
wenn über die Aufteilung des gesamten Handelsgewinns hier nichts gesagt wird.
Bevor auf die allgemeinere Ableitung komparativer Kostenvorteile eingegangen
wird, ist es hilfreich einige Grundüberlegungen anhand eines Zahlenbeispiels
nachzuvollziehen.
Wenn Robinson im angegebenen Zahlenbeispiel seine Nahrungsproduktion um eine
Einheit reduziert und eine zusätzliche Einheit Kleidung herstellt, dann
gewinnt er eine Stunde Freizeit. Umgekehrt erzielt Freitag zwei Stunden
Freizeit, wenn er umgekehrt eine Einheit Kleidung weniger produziert und dafür
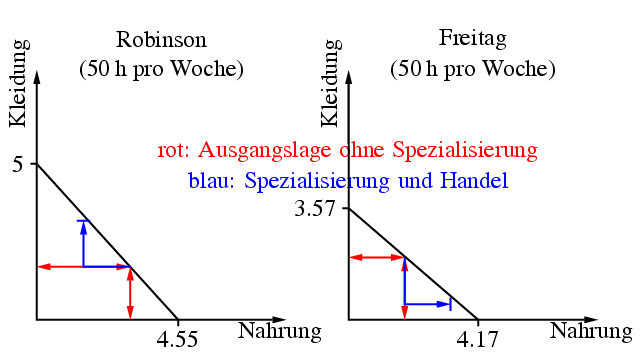
eine Nahrungseinheit mehr. Tauschen die beiden nur eins zu eins Kleidung gegen
Nahrung, wie in der folgenden Abbildung, dann konsumieren sie dieselben Mengen
wie zuvor, aber sie arbeiten beide weniger. Die gewonnene Freizeit können sie
nun genießen oder die Produktion entsprechend ausweiten, um anschließend mehr
zu konsumieren.
Komparative Kostenvorteile.
Die genannten Vorteile lassen allgemeiner herleiten, indem man folgende
Relationen bildet.
|
|
10
11
|
< |
1
1
|
< |
14
12
|
Einheiten: |
AE/KE
AE/NE
|
= |
NE
KE
|
|
|
Dabei stehen links und rechts in der Ungleichung die
sogenannten Grenzraten der Transformation: Wenn
Robinson die Herstellung von Kleidung um eine Einheit erhöhen möchte,
kann er die 11 benötigten Arbeitsstunden (AE = Arbeitseinheit) erzielen,
indem er die Produktion von Nahrungsmitteln einschränkt; damit bewegt er
sich auf der Transformationskurve! Er muss folglich of 10/11
Nahrungseinheiten (NE) je Kleidungseinheit (KE) verzichten. Die gleiche
Überlegung führt bei Freitag zu einer Erhöhung um 14/10 Nahrungseinheiten je
ausgelassene Kleidungseinheit. Jedes Tauschverhältnis (hier 1:1), das
zwischen den beiden Verhältnissen liegt, impliziert also einen gemeinsamen
Gewinn von +14/10-10/11 Nahrungseinheiten bei konstanter Zahl von
Kleidungsstücken (+1-1). Da Freitag eine Nahrungseinheit abgibt, beträgt
sein Handelsgewinn 14/10-1=4/10. Robinsons Vorteil ist kleiner, aber immerhin
positiv; er erhält eine Nährungsmitteleinheit, so dass sein Gewinn
1-10/11=1/11 lautet.
Fazit.
Die Argumentation für den Nachweis komparativer Kostenvorteile hängt
nicht von den Zahlenwerten ab, sondern ist allgemein gültig. Über die
Verteilung des Gewinns wird keine Aussage getroffen. Wichtig ist nur, dass
beide Parteien einen positiven Handelsgewinn realisieren können.