Walras-Gesetz
Das Walras-Gesetz besagt für das mikroökonomische Totalmodell, dass der Gesamtwert aller Überschussnachfragen nach sämtlichen Gütern stets den Wert Null hat. Demnach gilt: "Sind n-1 Märkte im Gleichgewicht, so ist auch der n-te Markt im Gleichgewicht". Beispiel für eine Tauschwirtschaft mit zwei Haushalten $A$ und $B$ sowie zwei Gütern $x_1$ und $x_2$. Für die Anfangsausstattungen $(w_{1A}, w_{2A})$ und $(w_{1B}, w_{2B})$ der beiden Haushalte resultieren zwei Probleme der Nutzenmaximierung \begin{eqnarray*} &&\max\left\{ u_A(x_{1A},x_{2A}) |\ p_1x_{1A} + p_2x_{2A} \leq p_1w_{1A} + p_2w_{2A} \right\}\\ &&\max\left\{ u_B(x_{1B},x_{2B}) |\ p_1x_{1B} + p_2x_{2B} \leq p_1w_{1B} + p_2w_{2B} \right\} \end{eqnarray*} mit den individuellen Nachfragefunktionen ( → Nutzenmaximierung) \begin{eqnarray*} x_{1A}^* = x_{1A}^M(p_1,p_2,w_{1A},w_{2A}) &\quad\text{und}\quad& x_{2A}^* = x_{2A}^M(p_1,p_2,w_{1A},w_{2A})\\ x_{1B}^* = x_{1B}^M(p_1,p_2,w_{1B},w_{2B}) &\quad\text{und}\quad& x_{2B}^* = x_{2B}^M(p_1,p_2,w_{1B},w_{2B}). \end{eqnarray*} Zusammen mit den Gleichgewichtsbedingungen \begin{eqnarray*} x_{1A}^* + x_{1B}^* = w_{1A} + w_{1B}\\ x_{2A}^* + x_{2B}^* = w_{2A} + w_{2B} \end{eqnarray*} liegen 6 Gleichungen zur Bestimmung von 6 Variablen ($x_{1A}^*$, $x_{2A}^*$, $x_{1B}^*$, $x_{2B}^*$, $p_1$, $p_2$) vor. Allerdings ist bekannt, dass wegen der Freiheit von Geldillusion sämtliche Nachfragefunktione homogen vom Grade null in den Preisen $p_1$ und $p_2$ sind. Damit enthalten die Nachfragegleichungen nur noch einen Relativpreis $p_1/p_2$ statt zweier Geldpreise $p_1$ und $p_2$. Wählt man das zweite Gut als numéraire mit dem willkürlich festgelegten Preis $p_2=1$ so ergibt sich mit \begin{eqnarray*} x_{1A}^* = x_{1A}^M(p_1,w_{1A},w_{2A}) &\quad\text{und}\quad& x_{2A}^* = x_{2A}^M(p_1,w_{1A},w_{2A})\\ x_{1B}^* = x_{1B}^M(p_1,w_{1B},w_{2B}) &\quad\text{und}\quad& x_{2B}^* = x_{2B}^M(p_1,w_{1B},w_{2B}) \end{eqnarray*} zunächst ein System aus 6 Gleichungen mit 5 Variablen ($x_{1A}^*$, $x_{2A}^*$, $x_{1B}^*$, $x_{2B}^*$, $p_1$). In der Tat hat Walras gezeigt, dass eine der Gleichungen redundant ist. Dazu ist zu beachten, dass beide Haushalte implizit ihr Budget vollständig ausschöpfen. Also gilt \begin{eqnarray*} p_1x_{1A}^* + p_2x_{2A}^* = p_1w_{1A} + p_2w_{2A}\\ p_1x_{1B}^* + p_2x_{2B}^* = p_1w_{1B} + p_2w_{2B} \end{eqnarray*} Summiert man diese Budgetgleichungen, so folgt \[ p_1 \left[ x_{1A}^* + x_{1B}^* - w_{1A} - w_{1B} \right] + p_2 \left[ x_{2A}^* + x_{2B}^* - w_{2A} - w_{2B} \right] = 0 \] In den eckigen Klammern steht die individuelle Überschussnachfrage nach dem jeweiligen Gut. Ist die Überschussnachfrage nach dem ersten Gut gleich null (d.h. $x_{1A}^* + x_{1B}^* - w_{1A} - w_{1B} = 0$), dann muss auch der zweite Markt im Gleichgewicht sein. Folglich ist eine der Gleichgewichtsbedingungen redundant, so dass 5 Gleichungen zur Bestimmung von 5 Variablen zur Verfügung stehen. Alternativ kann man die Gütermengen mit Hilfe der Nachfragefunktionen eliminieren. Analog resultiert nun ein System aus 2 Gleichungen zur Bestimmung des Relativpreises $p_1$ \begin{eqnarray*} p_1 \left[ x_{1A}^M(\cdot) - w_{1A} \right] + \left[ x_{2A}^M(\cdot) - w_{2A} \right] = 0\\ p_1 \left[ x_{1B}^M(\cdot) - w_{1B} \right] + \left[ x_{2B}^M(\cdot) - w_{2B} \right] = 0, \end{eqnarray*} wobei eine der beiden Gleichunge auf Grund des Walras-Gesetzes redundant ist.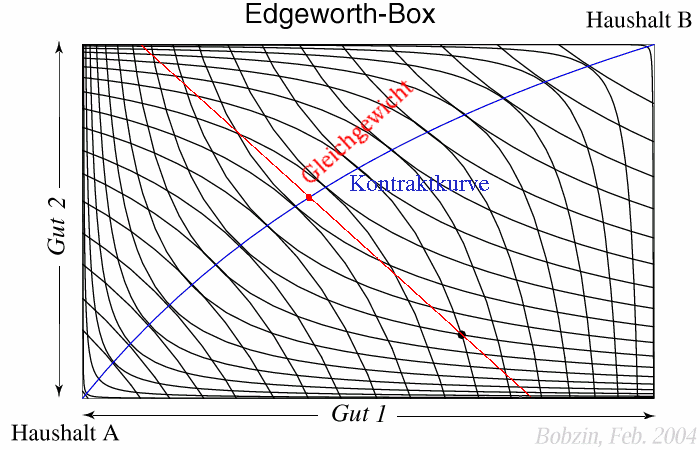
Freiheit von Geldillusion
Edgeworth-Tauschbox
Tauschkurven (grafische Bestimmung des Gleichgewichts)

