Der optimale Verbrauchsplan: Analytische Bestimmung
Nutzenmaximierung
ökonomisches Prinzip Problem der Maximierung einer Nutzenfunktion $u(x_1,x_2)$ unter der Nebenbedingung, dass die Ausgaben das gegebene Einkommen $y$ nicht übersteigen dürfen (Nebenbedingung als Ungleichung). \begin{eqnarray*} &&u(x_1,x_2) \to \text{Max.}\\ \text{u.d.NB.}\quad &&p_1x_1 + p_2x_2 \leq y\\ && x_1, x_2\geq 0 \end{eqnarray*} Grafische Darstellung der Lösung: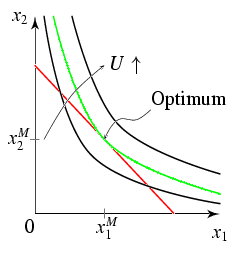
Parameter: $p_1$, $p_2$, $y$ sind zunächst als Konstante zu behandeln. Entscheidend: $\cL$ nimmt in Bezug auf $x_1$, $x_2$ das Maximum dort an, wo auch $u$ maximal ist (und umgekehrt). Die Kuhn-Tucker-Bedingungen lauten \begin{eqnarray*} \abl{\cL}{x_1} &\leq 0 && x_1^*\geq 0 && \abl{\cL}{x_1} x_1^*=0\\ \abl{\cL}{x_2} &\leq 0 && x_2^*\geq 0 && \abl{\cL}{x_2} x_2^*=0\\ \abl{\cL}{\lambda} &\geq0 && \lambda^*\geq0 && \abl{\cL}{\lambda}\lambda^*=0 \end{eqnarray*} Unterstellt man eine innere Lösung, also $x_1^*>0$ und $x_2^*>0$, dann muss \begin{eqnarray*} \abl{\cL}{x_1} &= \abl{u(x_1^*,x_2^*)}{x_1} - \lambda^* p_1 = 0\\ \abl{\cL}{x_2} &= \abl{u(x_1^*,x_2^*)}{x_2} - \lambda^* p_2 = 0 \end{eqnarray*} erfüllt sein. Nun lässt sich $\lambda^*$ eliminieren \[ \frac{{\partial}u/{\partial}x_1}{{\partial}u/{\partial}x_2} =\frac{p_1}{p_2} \quad\text{oder}\quad \frac{{\partial}u/{\partial}x_1}{p_1}= \frac{{\partial}u/{\partial}x_2}{p_2}=\lambda^* \] Folglich muss bei positiven Grenznutzen auch $\lambda^*>0$ gelten, so dass \[ \abl{\cL}{\lambda} = y - p_1x_1^* - p_2x_2^* = 0 \] Fazit: Bei positiven Gütermengen, verhalten sich die Grenznutzen wie die Güterpreise. Die rechte Aussage entspricht der modernen Fassung des 2. Gossenschen Gesetzes, wobei sich $\lambda^*$ als Grenznutzen des Geldes interpretieren lässt. Nachdem $\lambda^*$ eliminiert worden ist, liegen 2 Gleichungen mit 2 Variablen (nämlich $x_1^*$ ,$x_2^*$) vor: \begin{eqnarray*} \text{Tangentialpunkt}\quad &\text{GRS}=\frac{{\partial}u/{\partial}x_1}{{\partial}u/{\partial}x_2}=-\frac{\d x_2}{\d x_1}=\frac{p_1}{p_2}.\\ \text{auf der Budgetgleichung}\quad &y=p_1x_1^*+p_2x_2^* \end{eqnarray*} Beachte: Mit den Kuhn-Tucker-Bedingungen werden auch Ecklösungen erfasst, in denen entweder $x_1^*=0$ oder $x_2^*=0$ gilt. In diesem Fall liegt keine Tangentiallösung mehr vor.
- die optimalen Verbrauchsmengen oder auch Marshallschen Nachfragefunktionen \[ x_1^*=x_1^M(p_1,p_2,y) \quad\text{und}\quad x_2^*=x_2^M(p_1,p_2,y) \]
- den optimalen Wert des Lagrange-Multiplikators $\lambda^*=\lambda(p_1,p_2,y)$. (ökonomische Interpretation)
Arbeitsangebot

