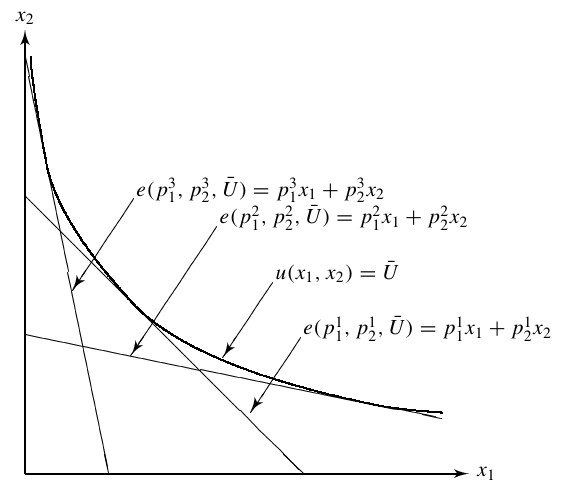
Duales Problem der Ausgabenminimierung
Ausgabenminimierung (duales Problem) Angenommen, man kennt die Ausgabenfunktion $e(\vp, U)$, die auf der Basis einer Nutzenfunktion $u(\vx)$ hergeleitet worden. \[ e(\vp,U)=\min_{\vx\geq\vO}\left\{\vp\trans\vx\ |\ U\leq u(\vx)\right\} \] Kennt man nur $e(\vp, U)$, dann stellt sich die Frage, was man implizit über die Nutzenfunktion $u$ weiß. Mit Hilfe der Dualitätstheorie lässt sich die Nutzenfunktion aus der Ausgabenfunktion (bei gewissen Regularitätsbedingungen) zurückgewinnen. Das entsprechende duale Problem basiert auf unendlich vielen Restriktionen für die Preise $\vp$: \[ u(\vx) = \max \left\{ U\ |\ e(\vp, U)\leq \vp\trans\vx \quad \forall \vp\geq \vO \right\} \] Um sich vorstellen zu können, wie das Problem "arbeitet", stelle man sich einen Ball vor. Dieser Ball wird nun durch sämtliche ihn tangierenden Ebenen (genauer alle Halbräume, die den Ball enthalten) beschrieben. Das Konstruktionsprinzip lässt sich graphisch veranschaulichen, wenn man sich bei der gewonnenen Nutzenfunktion $u$ auf ein Nutzenniveau $\bar U$ konzentriert. Aus den unendliche vielen Restriktionen sind hier nur die interessant, die die Indiffernzkurve $\bar U$ tangieren.