Die optimale Faktorkombination: Analytische Bestimmung der
Maximalproduktkombination (MPK)
ökonomisches Prinzip
Restriktion als Ungleichung
Ausgangspunkt ist das Problem der Maximierung des Outputs $x(v_1,v_2)$
(
Produktionsfunktion)
unter der Nebenbedingung einer gegebenen Kostensumme $c$, wobei die
Nebenbedingung als Gleichung vorliegt.
\begin{eqnarray*}
&&x(v_1,v_2) \to \text{Max.}\\
\text{u.d.NB.}\quad &&q_1v_1 + q_2v_2 = c \quad\text{Isokostengerade}\\
&&v_1, v_2\geq 0
\end{eqnarray*}
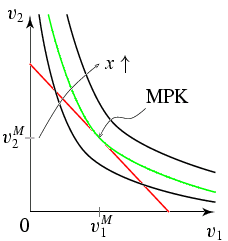
Grafische Darstellung der Lösung:
Lagrange-Ansatz
\[
\cL(v_1,v_2,\lambda) = x(v_1, v_2) + \lambda (c - q_1v_1 - q_2v_2)
\]
Unbekannte: $v_1$, $v_2$, $\lambda=$ Lagrange-Multiplikator
Parameter: $q_1$, $q_2$, $y$ sind zunächst als Konstante zu behandeln.
Entscheidend: $\cL$ nimmt in Bezug auf $v_1$, $v_2$ das Maximum dort an, wo
auch $x$ maximal ist (und umgekehrt).
- Bedingungen 1. Ordnung oder Lagrange-Bedingungen: partielle Ableitungen
gleich Null setzen.
Damit erhält man ein Gleichungssystem aus 3 Gleichungen mit 3 Variablen
$v_1$, $v_2$ und $\lambda$.
- Bedingungen 2. Ordnung (Min. oder Max.): hier nicht berücksichtigt!
Notwendige Bedingungen 1. Ordnung (3 Gleichungen, 3 Variablen)
\begin{eqnarray*}
\abl{\cL}{v_1} &\ =\ & \abl{x(v_1^*,v_2^*)}{v_1} - \lambda^* q_1 = 0\\
\abl{\cL}{v_2} &\ =\ & \abl{x(v_1^*,v_2^*)}{v_2} - \lambda^* q_2 = 0\\
\abl{\cL}{\lambda} &\ =\ & c - q_1v_1^* - q_2v_2^* = 0
\quad\text{Nebenbedingung des Problems}
\end{eqnarray*}
Aus den beiden ersten Gleichungen lässt sich $\lambda^*$ eliminieren
\[
\frac{{\partial}x/{\partial}v_1}{{\partial}x/{\partial}x_2}\ =\ \frac{q_1}{q_2}
\quad\text{oder}\quad
\frac{{\partial}x/{\partial}v_1}{q_1}\ =\ \frac{{\partial}x/{\partial}v_2}{q_2}\ =\ \lambda^*
\]
Die Grenzproduktivitäten verhalten sich wie die Faktorpreise. Oder äquivalent,
Gleichheit der
Grenzerträge des Geldes $= \lambda^*$.
Also liegen 2 Gleichungen mit 2 Variablen (nämlich $v_1^*$ ,$v_2^*$) vor:
\begin{eqnarray*}
\text{Tangentialpunkt}\ \
&&\text{GRS}\ =\ \frac{{\partial}x/{\partial}v_1}{{\partial}x/{\partial}v_2}\ = -\ \frac{\d v_2}{\d v_1}\ =\ \frac{q_1}{q_2}.\\
\text{auf der Isokostengeraden}\ \
&&c = q_1v_1^* + q_2v_2^*
\end{eqnarray*}
Aufgrund der Eigenschaften der Produktionsfunktion
(siehe GRS) und
der Kostengeraden (konstante Preise) liefert das
Gleichungssystem
- die optimalen Verbrauchsmengen (Maximalproduktkombination) oder auch die
Faktornachfragefunktionen
\[
v_1^* = v_1^M(q_1,q_2,c) \quad\text{und}\quad v_2^* = v_2^M(q_1,q_2,c)
\]
- den optimalen Wert des Lagrange-Multiplikators $\lambda^* = \lambda(q_1,q_2,y)$.
(ökonomische Interpretation)
Setzt man die Maximalproduktkombination in die Zielfunktion ein, dann ergibt
sich die
indirekte Produktionsfunktion
als Lösung des Problems.
\[
z(q_1,q_2,c)=q_1v_1^M(q_1,q_2,c)+q_2v_2^M(q_1,q_2,c)
\]
Expansionspfad (Variation des Kostensumme)