Konsumentenrente
Die
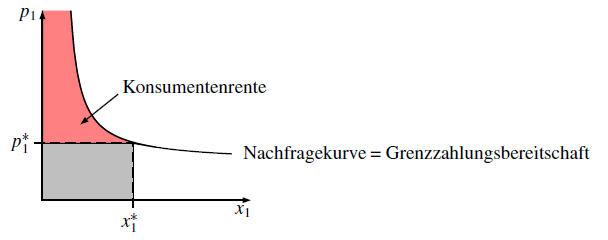
Konsumentenrente (consumer's surplus) lässt sich
interpretieren als die Differenz zwischen dem, was der Konsument maximal
bereit ist, für eine Menge
x zu bezahlen, und dem, was er am Markt
tatsächlich zahlen muss. Hierzu wird jeder Punkt auf der Nachfragekurve
als
Grenzzahlungsbereitschaft gesehen, das heißt, jeder Punkt
bezeichnet den Preis, den der Konsument bereit ist, für die
letzte
nachgefragte Einheit zu bezahlen. Bei vollständiger Preisdifferenzierung würde
der Konsument jede Einheit entsprechend seiner Grenzzahlungsbereitschaft
kaufen, so dass die Fläche unter der Nachfragekurve von 0 bis $x_1^*$ die
gesamte
Zahlungsbereitschaft angibt. Tatsächlich zahlt der Konsument
immer nur den Marktpreis $p_1^*$. Die Differenz zwischen der hypothetischen
Zahlungsbereitschaft und den tatsächlichen Ausgaben $p_1^*x_1^*$ heißt
Konsumentenrente.
Analytischer Ausgangspunkt ist ein Haushalt, der den Preisen $\vp'$ und dem
Einkommen $y'$ gegenübersteht. Entsprechend der
indirekten Nutzenfunktion lautet sein
maximal erreichbares Nutzenniveau
\[
U'=v(\vp', y').
\]
Angenommen, der Preis des Gutes $j$ steigt von $p_j'$ auf $p_j''$
\[
\vp'=(p_1,...,p_j',...,p_n)
\ \to\
\vp''=(p_1,...,p_j'',...,p_n),
\]
dann stellt sich die Frage, wie groß der "Nutzenverlust" des Haushalts ist.
Entsprechend der
kompensierenden
Variation ist die Frage zu beantworten, um wie viel die Konsumausgaben steigen
müssen, damit das ursprüngliche Nutzenniveau $U'$ erhalten bleibt,
\[
e(\vp'', U') - e(\vp', U').
\]
Das Problem dieser Abschätzung besteht darin, dass das Einkommen $y$ (und damit
die Konsumausgaben) in Wirklichkeit konstant bleibt, $y=y'=y''$. Im Normalfall
wird also das Nutzenniveau fallen,
\begin{eqnarray*}
\Delta U = U' - U'' &&= v(\vp', y) - v(\vp'', y)\\
\text{und}\quad y' - y'' &&= e(\vp', U') - e(\vp'', U'') = 0
\end{eqnarray*}
Mit Hilfe der
metrischen Nutzenfunktion
lässt sich dieser Nutzenverlust auf zwei Arten monetär approximieren, wobei
jeweils vernachlässigt wird, dass das Einkommen konstant ist.
äquivalente Variation
\[
EV=e(\vp', U') - e(\vp', U'') = \mu(\vp'; \vp', y) - \mu(\vp'; \vp'', y)
= y - \mu(\vp'; \vp'', y)
\]
kompensierende Variation
\[
CV=e(\vp'', U') - e(\vp'', U'') = \mu(\vp''; \vp', y) - \mu(\vp''; \vp'', y)
= \mu(\vp''; \vp', y) - y
\]
Beide Approximationen haben den Nachteil, dass sie sowohl das Nutzenniveau
$U'$ als auch das Niveau $U''$ enthalten. Diesen Mangel kann man beseitigen,
indem man $y=e(\vp', U') = e(\vp'', U'')$ substituiert. Unter
Berücksichtigung von
Shephards Lemma folgt:
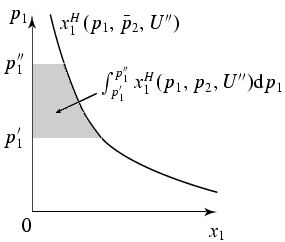
äquivalente Variation
\[
EV=e(\vp'', U'') - e(\vp', U'') = \int_{p_j'}^{p_j''} x_j^H(\vp, U'') \d p_j
\]
kompensierende Variation
\[
CV=e(\vp'', U') - e(\vp', U') = \int_{p_j'}^{p_j''} x_j^H(\vp, U') \d p_j
\]
Nun liegt es nahe, die
Konsumentenrente wie folgt zu
definieren:
\[
KR=\int_{p_j'}^{p_j''} x_j^M(\vp, y) \d p_j
\]
Würde die Marshallsche Nachfragefunktion $x_j^M$ denselben Verlauf wie
die Hickssche Funktion $x_j^H$ aufweisen, dann müsste $KR=CV$ oder $KR=EV$
gelten. Offensichtlich begeht man dabei einen Fehler, der zu Tage tritt, wenn
man die
Slutzky-Gleichung heranzieht.
\[
\abl{x_j^M(\vp, y)}{p_j}=\abl{x_j^H(\vp, U)}{p_j} - \abl{x_j^M(\vp, y)}{y}
x_j^H(\vp, U) \quad\text{mit}\ \ j=1,...,n
\]
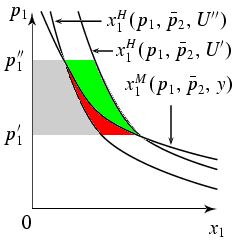
Handelt es sich bei $x_j$ um ein normales Gut, dann ist die Ableitung nach
dem Einkommen positiv, so dass die Hicksschen Nachfragefunktionen steiler
verlaufen muss als die Marshallsche Kurve. Bei vertauschten Achsenbezeichnungen
stellt sich die folgende Abbildung mit $ EV < KR < CV $ ein.
Zieht man schließlich
Roys Identität hinzu und
unterstellt eine Nutzenfunktion mit $\partial v/ \partial y =1$, so dass
\[
x_j^M(\vp, y)= - \frac{\partial v(\vp, y)/ p_j}{\partial v(\vp, y) / \partial
y} = - \abl{v(\vp, y)}{p_j},
\]
dann lässt sich die Konsumentenrente als Nutzenverlust interpretieren.
\[
KR=\int_{p_j'}^{p_j''} x_j^M(\vp, y) \d p_j = \int_{p_j''}^{p_j'} \abl{v(\vp,
y)}{p_j} \d p_j = v(\vp', y) - v(\vp'', y)
\]
Produzentenrente