Budgetrestriktion
Die
Budgetrestriktion gibt die objektiven
Entscheidungsmöglichen eines Haushalts an. Ein Güterbündel $(x_1,x_2)$ ist
genau dann zulässig, wenn die Ausgaben für das Güterbündel das gegebene Budget
oder Einkommen $y$ nicht übersteigen
\[
p_1 x_1 + p_2 x_2 \leq\ y,
\]
wobei die Gütermengen außerdem nichtnegativ sein müssen
\[
x_1\geq 0 \quad\text{und}\quad x_2\geq0.
\]
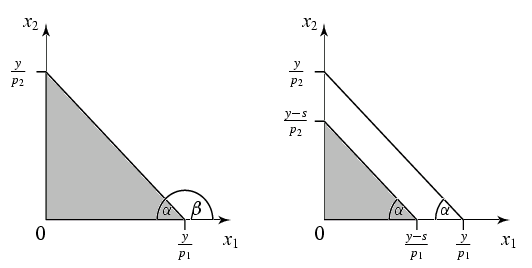
Wenn das Einkommen vollständig zu Konsumzwecken verwendet wird, die Ersparnis
s also gleich null ist, dann lautet der relevante Bereich der
Budgetrestriktion
\[
y = p_1 x_1 + p_2 x_2.
\]
Diese
Budget- oder
Bilanzgleichung wird auch
als Verbrauchsebene bezeichnet. Sie wird im Güterraum als Gerade
\[
x_2 =\ \frac{y}{p_2}\ -\ \frac{p_1}{p_2}\ x_1
\]
dargestellt, die eine negative Steigung hat.
\[
\tan \beta =\ \frac{\d x_2}{\d x_1}\ =\ -\ \frac{p_1}{p_2}\ =\ - \tan \alpha
\]
Bei
n Gütern kann die Budgetgleichung in Verktorschreibweise dargestellt
werden.
\[
y = \vp\T\vx = \sum_{j=1}^n p_jx_j
\]
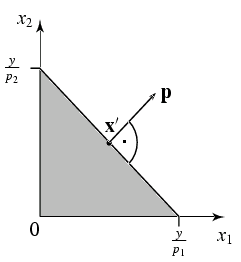
In Bezug auf den Güterraum steht der Preisvektor $\vp$ senkrecht auf der
Budgetgeraden an der betrachteten Stelle $\vx'$.